Quantum systems are more robust than previously thought, especially when weakly measured, with startling results. Dr. Mae-Wan Ho reports
In the standard quantum theory, a quantum system is in a superposition of states or in quantum entanglement (see Box), which is invariably destroyed by measurement. This is referred to as the ‘collapse’ of the wave function - of probability amplitudes - that defines the system, so the system ends up in one definite state and no other. In case of Schrödinger’s cat, this collapse of the wave function amounts to being found definitely dead or definitely alive.
Quantum superposition and quantum entanglement
‘Superposition’ and ‘entanglement’ are two of the strange properties of a quantum system. ‘Superposition’ refers to a quantum system existing simultaneously in multiple states, even states that, common sense tells us, are mutually exclusive. This is usually told as the parable of Schrödinger’s cat, shut up in a box with a vial of cyanide that at any moment might be triggered to release its deadly gas by a radioactive decay reaction. If the cat in the box were a quantum system, then before anyone raises the lid to look in, the cat would be described by a quantum ‘wave-function’ of complex quantum amplitudes, which have to be squared to give the usual probabilities (see "The quantum information revolution", this series). This puts the cat in a superposition of (classically) mutually exclusive states, simultaneously dead and alive, and all states in between.
As soon as it is ‘observed’ by opening the lid, however, the quantum superposition is destroyed, and the system’s wave function ‘collapses’ into a classical state. The cat is found either dead or alive.
‘Entanglement’ describes the way different particles can become correlated no matter how far apart they are, so that a measurement performed on one of them instantaneously determines the state of both the measured particle as well as the entangled particle. This too, collapses the wave-function that previously describes the complex probability amplitudes of the two particles together, no matter how far apart they are.
But could this interpretation be overly simplistic? First of all, the ‘collapse’ of the wave function only applies to the measured property of entangled states, while the unmeasured properties remain indeterminate. For example, a measurement to decide whether a particle is spin up or down leaves it and its entangled partner indeterminate as to whether the spin is oriented left or right.
Then, there are other recent indications that observation need not destroy entanglement.
Altewischer and coworkers in Leiden University in the Netherlands showed that entanglement between pairs of photons can survive even when one (or both) of the entangled photons is converted into a surface ‘plasmon’ and then back again into a photon.
Surface plasmons are oscillating electromagnetic fields strongly localized at the surface of a metal and associated with the collective motion of a large number of electrons. Surface plasmons are formed on metal films perforated by an array of holes smaller than the wavelength of the photons. The plasmon tunnels through the holes to form a similar plasmon on the other side, and eventually reconverts back into a photon.
Altewisher’s team sent many entangled photon pairs onto such metal films, and although many photons are lost as the result of absorption, the surviving photons remain entangled.
The state of a two-particle system is ‘entangled’ when its quantum-mechanical wave function cannot be factorised into two single-particle wave functions. This leads to one of the strangest features of quantum mechanics, non-locality. In other words, when one particle is measured to have a certain property, then the corresponding property of the other particle is instantaneously determined.
It is quite easy to get entangled photons, a starting photon can spontaneously split into a pair of entangled photons inside a nonlinear crystal.
Altewischer’s team wanted to find out what happens when entangled photons are sent through opaque metal films perforated with a periodic array of holes smaller than the wavelength of the photons. Will entangled photons survive such treatment and remain entangled? The answer is, surprisingly, yes.
First, they launched photons of one energy (one wavelength) into a crystal whose particular properties cause each photon to be split into two new photons, a process called down-conversion. By the conservation of energy, each down-converted photon has twice the wavelength and half the energy. Not only that, spin is conserved as well as energy, so the polarization of the two down-converted photons are always opposite to each other. For example, if one photon is measured to be linearly polarized in the vertical direction, the other photon will always be linearly polarized in the horizontal direction, and so on. It is as though the two photons know about each other instantaneously.
Altewischer’s team showed that the entanglement survives even when one (or both) of the entangled photons is converted into a surface ‘plasmon’ and then back again into a photon. Although many photons are lost as the result of absorption, the surviving photons are still entangled.
Given the collective nature of the surface plasmon, which involves some 1010 electrons, it seems remarkable that entanglement should survive. More surprisingly still, surface plasmon modes are short-lived, lasting for just a few femto-seconds (10-15s).
The key to surviving entangled, it seems, is to remain coherent by bouncing off other coherent systems.
In the commentary on the report, William Barnes of the University of Exeter in the UK pointed out that if we simply use a metallic mirror to reflect an entangled photon, we would expect entanglement to survive even though we would still be making use of the collective motion of many electrons to provide the reflection.
In both the surface-plasmon and simple reflection processes, we rely on the electron-electron scattering rate being low enough to allow the electron motion to remain coherent.
But there are even stranger quantum encounters in store.
Lucien Hardy, then at Oxford University in Britain, provided a beautiful illustration of the sort of paradox that arises in connection with quantum entanglement through a thought-experiment in 1992.
An entangled particle and anti-particle pair - an electron and a positron - is created and each flies off in the opposite direction. But their paths are made to cross at some point by strategically placed mirrors, and instead of annihilating each other as particle and antiparticle are supposed to do, they somehow manage to "be" and "not to be" at the same time and location.
Hardy considered a Mach-Zender Interferometer (MZI), a set-up containing a half-silvered mirror, which sends a quantum particle into a superposition of states, in that it travels down two separate arms at once: the transmitted and reflected paths.
The interferometer later reunites the two paths to meet at another half-silvered mirror, which is arranged so that if the particle has had an undisturbed journey - no encounter with any other particles or fields - it hits detector C. But if something disturbs the particle, it may hit a second detector, D.
What happens when two such interferometers positioned so that one arm of the first overlaps with one arm of the second (see Fig. 1)?
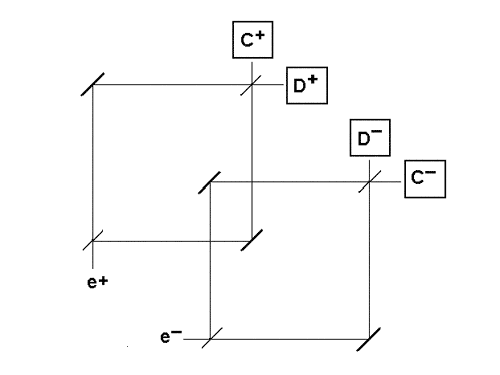
Figure 1. The overlapping paths of the electron and positron in an entangled pair
If a positron - the antiparticle of an electron – is sent through one interferometer, and an electron through the other at the same time, the two particles travelling along the overlapping arms should meet in an ‘annihilation region’ and destroy one another. Hardy showed that something much stranger happens: quantum theory predicts that both D detectors could click simultaneously. Somehow both particle and antiparticle could disturb each other, yet fail to annihilate, in the overlapping arms. This is Hardy’s paradox.
Most people tend to ‘resolve’ the paradox by pointing out that such paradoxes arise only because we make inferences that do not refer to results of actual experiments. And, if the actual measurements were performed, then standard measurement theory predicts that the system would have been disrupted in such a way that no paradoxical implications would arise.
But an international team of scientists led by Yakir Aharonov in Tel Aviv University, Israel, showed that Hardy’s thought experiment could be carried out, and that it could give new observable results, provided that weak measurements are made.
What would a weak measurement entail? It is one that does not disturb the system significantly, so it remains quantum coherent, and also sacrifices accuracy. According to Heisenberg’s uncertainty relations, an absolutely precise measurement of position reduces the uncertainty in position to zero, but produces an infinite uncertainty in momentum. But if one measures the position up to some finite precision, then one can limit the uncertainty in momentum to a finite amount.
Aharonov and his colleagues imagine such weak measurements are indeed possible, and ask what happens to Hardy’s paradox. They find the paradox far from disappearing. The results of their theoretical measurements turn out to be most surprising and to reveal a "deeper structure" in quantum mechanics, which makes it "even more paradoxical".
In the double MZI setup, it is arranged that if each MZI is considered separately, the electron can only be detected at C- and the positron only at C+. However, because there is a region where the two particles overlap, there is also the possibility that they will annihilate each other.
But the clicking of D- and D+ would be paradoxical. If D- clicked, that means the positron must have gone through the overlapping arm, otherwise nothing would have disturbed the electron, which would have gone to C-. The same logic applies if D+ clicked, that means the electron must have gone through the overlapping arm to disturb the positron. But, there has been no annihilation in either case, which is paradoxical.
Alternatively, if D- has clicked, the positron must have gone through the overlapping arm. But since there was no annihilation, the electron must have gone through the non-overlapping arm. The clicking of D+ indicates that the electron must have gone through the overlapping arm, and the positron the non-overlapping arm. But these two statements are contradictory, which ends in paradox again.
So far, these statements are based on no measurements being made as to which arm the positron or electron actually went. If a standard detector is put in the path of the electron in the overlapping arm, we can find the electron there, but the measurement itself disturbs the path, so the electron could end up in D- detector even if no positron were present. The paradox disappears.
Weak measurements however, will give different predictions. The weak measurement does not disturb the system significantly, but it will be imprecise. To make up for this, the measurement has to be repeated many times in order to get as close to the real answer as possible. (Alternatively, they can do the experiment with a large number of electron-positron pairs and measure the total number of electrons or positrons that go through each arm.) And to simplify the measurements, they concentrate only on the results when D- and D+ both click. The measurements, being weak can be made simultaneously without disturbing the system or each other.
The results – based on calculating the probabilities from the complex quantum amplitudes - show that indeed, the electron and positron, each has a probability 1 of being in the overlapping region, and a probability of 0 of being in the non-overlap region. But they could not both be in the overlapping region; and quantum mechanics is consistent with this too – the joint probability of both being in the overlapping region is 0.
Intuitively, the positron must have been in the overlapping arm otherwise the electron could not have ended at D- and, further, the electron must have gone through the non-overlapping arm as there was no annihilation. This is confirmed by the joint probability of positron being in the overlapping arm and electron in the non-overlapping arm equals to 1. Similarly, D+ clicking means that the electron must have been in the overlapping arm otherwise the positron could not have ended at D+, and further, the positron must have gone through the non-overlapping arm as there was no annihilation. The joint probability of the positron being in the non-overlap region and electron in the overlap region, too, is equal to 1. But these two statements are at odds with each other, as there was only one positron-electron pair. Quantum mechanics solves this paradox by having the joint probability of electron and positron being both in the non-overlapping branch equal to –1! That is being not merely absent, but negatively present.
Finally, "the electron did not go through the non-overlapping arm as it went through the overlapping arm" is also confirmed – a weak measurement finds no electrons in the non-overlapping arm, the probability of electron being in the non-overlapping arm equals to 0. But we know that there is an electron in the non-overlapping arm as part of a pair in which the positron is in the overlapping arm, as the joint probability of that is equal to 1. How is it possible to find no electrons in the non-overlapping arm? The answer is given by the existence of the –1 joint probability of both electron and positron pair in the non-overlapping arms, bringing the total number of electrons in the non-overlapping arm to zero! So the negative presence cancels out the positive presence, resulting in absence.
Klaus Molmer of Aarhus University in Denmark, initially sceptical, now thinks he knows how to do actual weak measurements. He suggests probing the locations of a pair of ions that are first cooled down to their lowest energy state, then hit with two carefully engineered laser pulses to send them into a superposition, which would move them to positions they should never occupy. He set up the ions so they will always fluoresce, except when they are in this paradoxical superposition. As soon as the fluorescence vanishes, he carries out a weak measurement on the ions’ position using another laser. The centre of mass should lie somewhere between the pair.
But the weak measurements show that, in the paradoxical quantum state, the ions’ centre of mass actually lies outside this region.
Molmer thinks that most of what has been done to-date with quantum systems employs weak measurement, only physicists haven’t realised it. And it could have practical consequences. For example, they could expose flaws in quantum cryoptography, in which it has always been supposed that disturbance caused by measurement would prevent eaves droppers decoding messages (see "Quantum information secure?" this series). But an eavesdropper who uses weak measurement would escape detection, and hence succeed in breaking the code.
All in all, reality is stranger, much stranger than we can imagine. I particularly like the idea of being positively present, absent, or negatively present simultaneously.
Article first published 18/03/04
Comments are now closed for this article