The Feynman Processor : Quantum Entanglement and the Computing Revolution, by Gerard J. Milburn, Perseus Books, Cambridge, Mass, 1998, ISBN 0-7382-0173-1. Dr. Mae-Wan Ho reviews.
My father has become an internet user at age 81. He sends me messages containing the latest digital family photographs, so I can see how he is putting on weight and regaining his health after a recent illness, and I can reply to tell him so immediately. He likes e-mail because it is so much faster than airmail and he can reach me when he doesn’t know where I am. He would be astonished to hear that scientists are still trying to make computers go even faster as well as smaller. And that we might be able to communicate faster than light using a quantum computer.
At the end of 1996, Intel Corporation, in collaboration with the United States Department of Energy (DoE) announced the first ‘ultra-computer’ to reach one trillion (10 to the power 12) operations per second, or one ‘teraflop’. It cost $55 million. The full system consists of 76 large cabinets with 9072 Pentium Pro processors and nearly 6 billion bytes of memory. The ultra-computer is the product of DoE's Accelerated Strategy Computing Initiative (ASCI), and would ultimately reach a peak performance of 1.8 teraflops. ASCI is a ten-year program to move nuclear weapons’ design and maintenance from being test-based to simulation-based. Were it not for the ultra-computer, Clinton would not have been able to sign the Comprehensive Test Ban Treaty on 25 September 1996.
But could a computer simulate reality perfectly? Is it possible that the DoE's confidence in the ultra-computer is misplaced? The quest for yet faster computers did not stop there.
IBM's computer, Deep Blue, defeated world chess champion Gary Kasparov in 1998, by sheer force of speed in checking the possible moves ahead. It can calculate 50 to 100 billion positions in three minutes, the time allowed for moves in major tournaments. It was a landmark victory, but it is clear that Deep Blue won not because it is cleverer than Kasparov. A computer just isn’t ever clever, at least, not clever enough. There are lots it can’t do. It doesn’t know to laugh at jokes, or feel sad. It can’t even walk into a MacDonald's on the high street to order a hamburger.
And it will be 2005 before a computer will attempt to simulate a protein molecule folding into shape. A new supercomputer, Blue Gene, costing $100 million, will be equipped with SMASH (simple, many and self-healing), which will dramatically simplify the use of instructions carried out by each processor. Instead of a single microprocessor on a chip, Blue Gene's chips will hold 32 processors and about a million microprocessors, so it will perform one quadrillion (10 to power 15) operations per second, or a ‘petaflop’. Even then, it will take a year to simulate an average protein folding, a process that's complete in split seconds in the body.
So, speed doesn’t make up for the fact that reality may be quite different, and works on different principles.
It was Alan Turing, inventor of the universal Turing machine, the direct precursor of the modern computer, who first cast doubt on the computer's ability to simulate reality. Turing proved, devastatingly, that the Turing machine can’t tell whether it can produce an answer to a problem in principle. Given a problem, the machine could run for a while and come to a stop, when it will have produced an answer, or else it could run forever.
Turing proved a theorem that says there is no general algorithm (a logical step by step procedure) which will determine if a Turing machine working on an arbitrary input is going to finish or run forever.
The Turing machine is a classical clockwork machine. What if there is another kind of machine? Enters the quantum computer. David Deutsch, theoretical physicist at Oxford University, thinks reality can in principle be simulated provided the universal machine is a quantum computer. And so does Gerald Milburn, Professor of Theoretical Physics, University of Queensland Australia, a key scientist in the effort to make a quantum computer, who has written an excellent book to tell us why.
A quantum computer can do things a classical computer cannot do. To simulate a system of N particles moving randomly, it would take a time that scales as NN, ie, exponential in the size of the system. For 10 particles, the ultra-computer working at 1 teraflop will take about three years just to compute the first time step. A quantum computer, on the other hand, will produce an arbitrarily accurate simulation of a quantum physical system. Similarly, the fastest computer will need billions of years to find the prime numbers, that multiplied together, result in a number containing 400 digits; whereas a quantum computer could finish the job in a year.
To see how quantum computing differs from classical computing, we need to understand the fundamental difference between the randomness of an ordinary coin-toss and that of a quantum coin-toss. And here is where Milburn's exposition is admirable. This book really rewards the diligent reader with critical understanding, unlike too many popular science books that obfuscate with over-simplification.
The classical probability of coming up head (H) or tail (T) in a single coin-toss is 0.5. If you toss the coin twice, there are four possible outcomes: HH, TT, HT and TH, the probability of each result being 0.5 x 0.5, or 0.25.
The quantum equivalent of a coin-toss is a light beam striking a half-silvered mirror, or beam splitter, where half of it is transmitted and half reflected. When the intensity of light is reduce sufficiently, single photons (irreducible quanta of light) strike the beam splitter, one at a time. Photon detectors placed in the path of the transmitted and the reflected photons will show that approximately half of the photons are transmitted (T) and half of them reflected (R). If instead of the photon detector, a fully reflecting mirror is placed in the path of the reflected and transmitted light respectively, the beam can be sent through a second beam splitter. This is equivalent to a second coin-toss. So, in analogy to the classical coin-toss, there are four possible paths for a photon, TT, RR, TR and RT. In the arrangement of Figure 1, paths TT and RR will end up in the upper (U) detector, whereas TR and RT will end up in the lower (L) detector. So, just as in the classical coin- toss, the U and L detectors will each detect half of the photons.
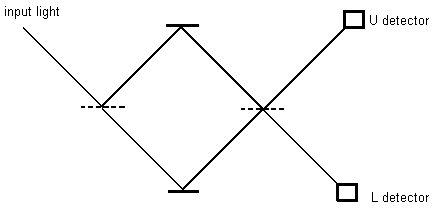
However, if we have certain knowledge that the photon is reflected or transmitted after the first beam splitter, ie, if we observe, then the number of photons registered by the U or L detectors will no longer be half. That is the first sign of quantum strangeness.
So far, we have been treating the light beam as if it were a stream of particles, which it is not. Light is simultaneously both wave and particle. This becomes evident as the relative light paths in the upper and lower half of the figure is altered, so that the light waves can interfere destructively with each other. It can be arranged that no light reaches the U detector, or the paths can be adjusted so that U receives say 20% of the light and L 80% of the light. But when the intensity of the light beam is reduced so that only single photons strike the beam-splitter at a time, all the photons will be registered by the U detector, or the U detector and L detector will register 20% and 80% of the photons respectively. It is as if the individual photon can still interfere with itself, as though it were a wave.
This strange behaviour of light can be perfectly described by considering probability amplitudes instead of probabilities, and probability amplitudes change when unobserved, indistinguishable alternatives become distinguishable. And this can lead to paradoxical situations such as quantum ‘seeing in the dark’, or getting information about something without light ever reaching it.
Probability amplitudes give probabilities when squared, and the rule for combining them was discovered by quantum physicist Richard Feynman. Feyman's rule says that if an event can happen in two or more indistinguishable ways, the probability amplitude for that event is the ‘sum’ of the probability amplitudes for each way considered separately. The final probability of an event is then obtained by the sum of the squares of the two numbers describing the resultant probability amplitude.
Feynman's rule is Pythagora's theorem: a2 + b2 = c2, which tells us how to obtain the length of the hypotenuse of a right-angled triangle from the lengths of the two sides. We learned that in elementary Euclidean geometry in school. It seems that Euclidean geometry enters fundamentally into quantum reality. But why should that be? "Nobody knows how it can be like that," said Feynman.
An ordinary coin-toss provides one bit of information, yes or no. Its quantum counterpart, however, provides anything from one bit to infinity, depending on how many indistinguishable possibilities are generated by beam splitters placed in the path of the photon. To capture this difference, Bill Schumaker coined a new word, qubit. "A qubit is infinity in a coin toss."
Now, add quantum entanglement, the correlation between subsystems in a state of quantum superposition, to Feynman's rule and one comes up with still stranger stuff, the e-bit, or information transfer through the entangled state, the possibilities of quantum crytography, teleportation (beam me up Scotty), and quantum computing.
The popular parable of the entangled state is Schrödinger's cat, which is in superposition of being both dead and alive at the same time. In fact, Feynman's rule already describes the superposition of indistinguishable alternatives, ie, the entangled state.
Quantum computing depends above all, on the coherent entangled state, or pure state that contains the superposition of multiple, even mutually exclusive alternatives. The more alternatives are entangled, the faster the quantum computing. It is the ability to ask many questions all at once, rather than one question at a time.
The theory of quantum computing is well advanced, but no quantum computer has yet been built. The Department of Defence is supporting a lot of work in this area, perhaps as part of star-wars weaponry. Different bits of hardware are used to create entangled states. These include single ions trapped in a strong electric field, atoms trapped in tiny optical cavities, and nuclear magnetic resonance to create superposition of spins of atomic nuclei in organic molecules such as chloroform. One major problem is decoherence, or loss of coherent superposition, which would make the computer stop working.
Are quantum physicists looking in all the right places? I have proposed, some time ago, that quantum coherence is the basis of living organisation (see "Science and Ethics in a New Key", this issue). The coherence of organisms is actively maintained, and extends, in the ideal, over all space-time scales. Could the organism be the model of the quantum computer that quantum physicists are trying to build? Could it be that proteins in the body fold to perfection in split seconds because the process involves quantum computing via infinitely many entangled states that encompass the entire body?
Can a quantum computer simulate reality perfectly? Milburn asserts that "the physical world is a quantum world", which makes "a quantum computer not only possible, but inevitable." I agree only in the sense that the organism may already be a kind of quantum computer.
Milburn goes further, he says it may take decades or perhaps a century, but "a commercially viable quantum computer is a certainty." I am not so sure of that.
Certainly, a quantum computer could solve what a classical computer cannot solve. But Milburn and others believe that only will the quantum computer be able to simulate reality, it will be part of the fabric of reality. That should send chills up and down our spine.
Will a quantum hyper-computer take over the world? Will it simulate a human being so exactly that it is a hyper-intelligent human being? Well, if it starts to laugh at jokes I’d be worried. And if it can really simulate perfectly a human being, we better start setting a good example. Otherwise it has every chance of turning out to be a power-hungry despot intent on enslaving the whole world.
Article first published 15/10/01
Comments are now closed for this article