Neuronetwork World 5, 733-750, 1995.
The problem of living organization can be stated as follows: how is it that an organism consisting of a multiplicity of tissues and cells and astronomical numbers of molecules of many different kinds can develop and function as a whole? How does the organism manage to have energy at will, whenever and wherever required, and in a perfectly coordinated way? One idea that has emerged over the past 20 years is that it is coherent. While the meaning of coherence is unambiguous within quantum theory, difficulties arise when we try to apply the concept to a complex living system with a highly differentiated space-time structure.
The coherence of the organism can most easily be appreciated by a recently developed noninvasive technique that allows one to see the whole organism down to the details of the molecules that make up its tissues. Brilliant interference colours are produced by recombining plane-polarized light split up into slow and fast rays on passing through birefringent liquid crystalline regimes (Fig. 1).1 The principles involved are the same as those used in identifying mineral crystals in geology. Different tissues appear in different colours and varying in intensity according to the orientation and birefingence of the molecules involved as well as their degree of order. The organism - in this case a Drosophila larva about to emerge - is obviously alive. Waves of muscle contraction are sweeping over its body, so one can infer that all the molecular motors and enzymes in the tissues are busily turning and deforming as energy is transformed, so how is it possible that they have a crystalline order? It is most likely because the molecular motions are highly correlated or coherent. As visible light is about 1014 hz, and correlated molecular motions generally less than 1010hz, the tissues will appear indistinguishable from static crystals to the light passing through so long as the movements of their constituent molecules are coherent. With this imaging technique, one can see that the movements of the organism are fully coordinated at all levels from the macroscopic to the molecular, and that is what the coherence of the organism entails.
This image also brings out the wholeness of the organism. The Drosophila larva - like all other animals from protozoa to vertebrates without exception - is polarized along the anteroposterior axis, as though the entire organism is one uniaxial crystal. This leaves us in little doubt that the organism is a singular whole, despite the diverse multiplicity of its constituent parts.
I mentioned that the molecules of the tissues maintain their crystalline order when they are actively transforming energy. The evidence suggests that the crystalline order is dependent on energy transformation, so that the more energetic the organism, the more intensely colourful it is, implying that the molecular motions are all the more coherent.(2) This is consistent with ultrasensitive high-speed measurements of contracting muscles which show all the molecular motors cycling in synchronous steps.(3,4) Similarly, X-ray diffraction reveals that a high degree of supramolecular order is maintained during isometric contraction.(5) The coherence of the organism is therefore closely tied up with its energetic status. To be precise, it is tied up with the way energy is stored and readily mobilized over all its space-time domains.
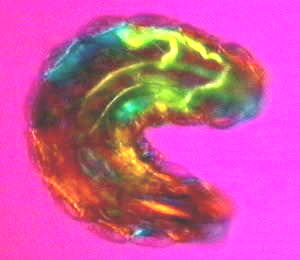
Figure 1. Live first instar Drosophila larva observed with a noninvasive imaging technique that produces interference colours in its tissues depending on the birefringent, liquid crystalline order of the constituent molecules.(1)
The problem I address in this paper is how to understand the coherence of organisms in terms of energy relationships as revealed by thermodynamics and quantum theory. Some of the arguments are given elsewhere,(6-8) though none of them as yet complete or fully coherent.
The first thermodynamic characteristic of an organism is that it is not a heat engine. It is to all intent and purposes an isothermal system, which means that strictly speaking, no work can be done by heat transfer, as that requires a temperature gradient. What kind of 'engine' is the living organism? Harold Morowitz(9) considers 4 types of engines (Fig. 2). The first three, the Carnot engine, the industrial engine and the fuel cell, are all equilibrium devices. As the first two engines operate by heat transfer, they are ruled out. That leaves the third, the chemical fuel cell and the fourth, the far from equilibrium machine, both promising candidates for the living system.
Figure 2. Four types of engines. Carnot and industrial engines depend on heat exchange. The fuel cell and the far from equilibrium engines do not depend on the conversion of energy into heat. The incomplete arrows leading from the fuel cell and far-from equilibrium engines to the heat sink indicate that the heat loss is not a necessary part of the working cycle.
The living system is remarkable for its efficiency and rapidity of energy transformation. The first clue to its efficiency is offered by analogy to the equilibrium fuel cell, whose efficiency is given by
Eff. = 1 - TDS/DU (1)
where DS and DU are the changes in internal entropy and energy and T is the temperature of the surroundings. One way to be efficient is obviously to generate as little entropy as possible.
Does the living system tend towards the minimum of entropy production and maximum efficiency?
The rate of entropy production in the living system is equal to the rate of increase in entropy plus the rate of outflow of entropy,
rate of entropy production = rate of entropy increase in system + rate of entropy outflow
At steady state, the first term on the right is zero; however, that does not mean entropy production is minimum. As Denbigh(10) points out, the rate of entropy production may still be very large if the rate of entropy outflow is large. The rate of entropy production is only a minimum if energy transduction occurs at quasi-equilibrium, or in far from equilibrium conditions, as described later on.
Of equal importance to the efficiency of the living system is the minimalization of free energy dissipation, so that the quantity,
DG = DH - TDS (2)
approaches zero. There are two ways to achieve that.
The first, which is well-known and ubiquitous in metabolism, is to couple thermodynamic uphill reactions to the downhill ones, so that the negative free energy changes balance the positive ones. The second, not so well-known, is to couple energy transfer directly, by individual enzyme/protein molecules acting as 'molecular energy machines'. In other words, the energy is never thermalized before it is turned into work. Enzymes and proteins, by dint of their flexibility and size, can absorb energy from the site where it is released, store it, and deliver it directly by appropriate conformational changes to where it is used. This "conservation of free energy", according to Lumry,(11) is achieved via enthalpy-entropy compensation in different parts of the large macromolecule as it undergoes cooperative deformations and movements involving the whole macromolecule. According to Eq. (2), free energy change is the difference between the two terms,DH and TDS, which can therefore compensate for each other when enthalpy and entropy changes are of the same sign. At the appropriate temperature, Tc, the compensation temperature, which is generally found to be within the physiological range for many reactions,(11) the compensation is exact, and DG = 0. Thus, one can see that within the living system, positive entropy production can be linked to the generation of work by increasing enthalpy at the same time.
Enthalpy/entropy compensation and free energy conservation also takes place between different ezyme molecules in multienzyme complexes which engage in cooperative movements to channel metabolites in sequential reactions without releasing them into the 'bulk aqueous phase' (see below). By "dynamic matching of conformational fluctuations", the collective motions of the associated proteins are no longer independent, but become correlated as a whole.(11) This reciprocity in energy relationship will be especially favoured in the quasi-crystalline array of proteins in the membranes of the mitochondria and the chloroplasts, and also in the dense arrays of molecular motors in muscle. However, as I shall show later on, what is being conserved is not 'free energy' but stored energy.
Everyone knows that the living system is maintained far from thermo-dynamic equilibrium; because of that, its temperature does not uniquely define the energy content. Some people argue that the 'real' temperature of the living system must be thousands of degrees kelvin, but another way to describe the living system is that it has a very high heat capacity, or capacity for energy storage. Living systems store a great deal of energy, and both energy storage and efficiency of energy transformation are intimately linked in the space-time structure of living processes. It is that which enables organisms to adopt the most efficient modes of working in both equilibrium and non-equilibrium regimes.(6-8)
An organism is nothing if not organized heterogeneity, with nested dynamic structures over all space-time scales. The differentiation of the body into organs, tissues, and cells is familiar to everyone. The cell itself is partitioned into many compartments by cellular membrane stacks and organelles that can respond directly to external stimuli and relay signals to other compartments. Within each compartment, microcompartments can be separately energized to give local circuits; and single enzyme proteins, or complexes of two or more proteins can function as molecular energy machines that cycle autonomously without immediate reference to its surroundings.(8)
Spatial differentiation in the living system, therefore, spans at least ten orders of magnitude from 10-10 m for intramolecular interactions to metres for nerve conduction and the general coordination of movements in larger animals. The relaxation times of processes range from <10-14 s for resonant energy transfer between molecules to 107s for circannual rhythms. Something is surely missing from any account that treats the living system as though it has a single, homogeneous 'steady state'.
The physiologist Colin McClare, who was concerned to reformulate thermodynamics so that it could apply not just to statistical ensembles of molecules but to individual molecules, first introduced the important notion of a characteristic time of energy storage.(12) This characteristic interval of time t, at temperature q, partitions the energy of the system into thermal energies that reach equilibrium in a time less than t, and the stored energies that remain in a non-equilibrium distribution for a time greater thant. So, stored energy is any form which does not thermalize, or degrade into heat in the intervalt
The explicit introduction of time, and hence time-structure enables us to see that there are two quite distinct ways of doing useful work at maximum efficiency in the living system, not only slowly according to conventional thermodynamic theory, but also quickly - both of which are reversible and generate little or no net entropy. (This is implicit in the classical formulation, dSe0, for which the limiting case is dS=0. But the attention to time-structure makes much more precise what the limiting conditions are.)
A slow process is one that occurs at or near equilibrium. The efficiency as measured by Eq. 1 approaches 1 as DS approaches zero. By taking account of characteristic time, a reversible thermodynamic process merely needs to be slow enough for all thermally-exchanging energies to equilibrate, ie, slower than t, which can in reality be a very short period of time for processes that have short time constants. The effect of spatial partitioning - from compartments to microcompartments - is to restrict the volume within which equilibration occurs, thus reducing the equilibration time. This means that local equilibrium may be achieved for many biochemical reactions in the living system. We begin to see that thermodynamic equilibrium itself is a subtle concept, depending on the level of resolution of time and space.
At the other extreme, there can also be a process occurring so quickly that it, too, is reversible. In other words, provided the exchanging energies are not thermal energies in the first place, but remain stored, then the process is limited only by the speed of light. Resonant energy transfer between molecules is an example of a fast process. It occurs typically in 10-14s, whereas the molecular vibrations themselves die down, or thermalize, in 10-9s to 101s. It is 100% efficient and highly specific, being determined by the frequency of the vibration itself. This process is now known to be involved in the primary steps of photosynthesis where energy transfer and electron transfer occur with great speed and with almost 100% quantum yield.(13) Resonant energy may also be involved in muscle contraction as McClare has suggested. Recent evidence indicates that energy from a single molecule of ATP may be delocalized over 4 or more work cycles of the molecular motor(s).14
McClare restated the second law so that it could apply to single molecules, say, enzyme molecules acting as molecular energy machines: useful work is only done by a molecular system when one form of stored energy is converted into another. In other words, thermalized energy is unavailable for work and it is impossible to convert thermalized energy into stored energy.
McClare's restatement of the second law is unnecessarily restrictive, and possibly untrue, for thermalized energy from burning coal or petrol is routinely used to run machines such as generators and motor cars. Furthermore, when one takes the nested compartmental structure of the living system into account, then thermalized energies from a small compartment will still be contained within a larger encompassing compartment, so there is a possibility it may be available for work. For example, enzymes embedded in a membrane which can undergo cooperative correlated motions could channel thermal energies to enzymically active conformational changes. In other words, local temperature fluctuations within an isothermal system may perform work, which is not contrary to the second law, for the living system is not at thermodynamic equilibrium. I suggest a more adequate restatement of the second law as follows:(6,8)Useful work is done by molecules by a direct transfer of stored energy, and thermalized energy cannot be converted into stored energy in the same system. A 'system' is here defined by the extent to which thermal and other exchanging energies equilibrate within the relaxation time of the process involved. This also clearly demands a more specific definition of the spatial extent of equilibration, which is done below.
It is of interest to compare the thermodynamic concept of 'free energy' with the concept of 'stored energy'. The former is strictly an ensemble concept, it cannot be defined a priori, much less can it be assigned to single molecules, as even changes in free energy for an ensemble cannot be defined unless we know how far the reaction is from equilibrium. Thus, Lumry's "free energy conser-vation" is strictly speaking, stored energy conservation. Stored energy, as defined by McClare with respect to a characteristic time interval, can be extended to a characteristic spatial domain, so one can generalize the concept of energy stored within a characteristic space-time. Stored energy, therefore, depends explicitly on the space-time structure of the processes in the system, and it has meaning applied to whole organisms as to single molecular machines.(8) For example, energy is stored as bond vibrations or mechanical/electrical strains in protein molecules within a spatial extent of 10-9 to 10-8m and a characteristic timescale of 10-9 to 10-8s. For a human being, the overall energy storage domain is in metre-decades. In between these two extremes, energy is stored in nested spatiotemporal compartments which are locally in equilibrium, but globally out of equilibrium with respect to one another, with equilibration space-times spanning the whole gamut between the local and fast to the global and slow.
Energy is mobilized in living systems by coupled flows of metabolites. The flow of metabolites is coupled to a flow of electrons and protons up and down the electronic/protonic gradients via the interconversion of ATP and ADP. The energy of the photon absorbed by chlorophyll is coupled to electron transport. Electron transport is coupled to the translocation of protons across the energy transducing membrane. The proton gradient thereby created supplies the protonmotive force for the synthesis of ATP from ADP and Pi. And finally, the hydrolysis of ATP back to ADP and Pi is coupled to practically all thermodynamically uphill or energy requiring reactions. All coupled flows are vectorial, the flows are in the direction of their respective forces or gradients. In addition, two features may be noted.
First, the couplings are symmetrical for the most energetically efficient processes. It means that the forces have reciprocal effects on the coupled flows, and also, if the forces are reversed, so are the flows. This applies to ATP synthesis from ADP and Pi, coupled to proton transport in oxidative and photosynthetic phosphorylation; as well as ATP splitting coupled to the molecular motor in muscle contraction. ATP is split into ADP and Pi by the ATP synthase embedded in the membrane when the proton gradient is run in reverse, just as ATP is synthesized by the molecular motor when ADP and Pi are supplied.
The second notable feature of the coupled flows of energy and material is that they are cyclical, as a casual glance at a metabolic chart will convince us. Cycles differ in lengths from the tricarboxylic acid cycle of core metabolism to the relatively short redox cycles in the elements of the electron transport chain and the two state interconversions of intermediates such as NADH/NAD and ATP/ADP. Are the two features - symmetrical coupling and cyclical flows - predicted from thermodynamics? I believe so.
The quasi-equilibrium approximations of the steady state developed by Onsager(15) show how symmetrical coupling of linear processes can arise naturally in a system under energy flow. A system of many coupled processes can be described by a set of linear equations,
Ji = Sk LikXk (3)
where Ji is the flow of the ith process (i = 1, 2, 3.....n), Xk is the kth thermodynamic force (k = 1, 2, 3,.....n), and Lik are the proportionality coefficients (where i = k) and coupling coefficients (where i ` k). Onsager showed that for such a multi-component system, the couplings for which the Xks are invariant at microscopic level with time reversal (i.e., velocity reversal) will be symmetrical; in other words,
Lik = Lki (4)
The main difficulty in applying Onsager's result to the living system is that the latter is far from thermodynamic equilibrium and operating in the nonlinear regime, whereas Onsager's reciprocity relationship is only valid for the linear regime close to thermodynamic equilibrium. However, Onsager's reciprocity relationship has recently been generalized by Sewell(16) to nonlinear processes exhibiting space-time scale invariance. Those are the characteristics of a whole class of critical phase-transitions(17) that may well include the living system (see later). Symmetrical coupling will apply for as long as those coupled processes are dispersion free, and hence stable.
An archetype of such critical phenomena is the Bénard convection cells that arise in a pan of water heated uniformly from below. At a critical temperature difference between the top and the bottom, bulk flow begins as the lighter, warm water rises from the bottom and the denser, cool water sinks. The whole pan eventually settles down to a regular honeycomb array of flow cells. So long as the temperature difference remains, the cells are stably maintained as heat flow couples (symmetrically) to the bulk flow of water.
The condition of dispersion-free macroscopic observables is satisfied in a pure phase, which, as Sewell points out, is a preprequisite to any deterministic law including that of Onsager. Sewell's generalization of the Onsager reciprocity relationship applies to locally linearized combinations of forces, which nonetheless behave globally in nonlinear fashion. This is particularly relevant to the living system, where nested compartments and microcompartments ensure that many processes may be operating locally at thermodynamic equilibrium even though the system as a whole is far away from equilibrium. Also, as each process is ultimately connected to every other in the metabolic net through catenations of space and time, even if truly symmetrical couplings are localized to a limited number of metabolic/energy transducing junctions, the effects will be shared or delocalized throughout the system, so that the reciprocity relationship will apply to appropriate combinations of forces, precisely as formulated by Sewell.
Another important assumption which justifies the application of Onsager's relationship to the living system is that suggested by Denbigh.(10) It is to regard the system in question as a superposition of dissipative and non-dissipative processes, so that the Onsager relationship applies only to the latter. In other words, it applies to coupled processes for which the net entropy production is zero,
Sk DSk = 0 (5)
This will include most of what goes on in living systems because of the ubiquity of coupled cyclic processes, for which the net entropy production is zero, as expressed in Eq. (5).
The other important development in the thermodynamics of the steady state came from Morowitz, who derived a theorem showing that at steady state, the flow of energy through the system from a source to a sink will lead to at least one cycle in the system.(9) The proof goes as follows.
For a canonical ensemble of systems at equilibrium with i possible states, where fi is the fraction of systems in state i (also referred to as occupation numbers of the state i), and tij is the transition probability that a system in state i will change to state j in unit time. The principle of microscopic reversibility requires that every forward transition is balanced in detail by its reverse transition, ie,
fi tij = fj tji (6)
If the equilibrium system is now irradiated by a constant flux of electromagnetic radiation such that there is net absorption of photons by the system, i.e., the system is capable of storing energy, a steady state will be reached at which there is a flow of heat out into the reservoir (sink) equal to the flux of electromagnetic energy into the system. At this point, there will be a different set of occupation numbers and transition probabilities, fi' and tij'; for there are now both radiation induced transitions as well as the random thermally induced transitions characteristic of the previous equilibrium state. This means that for some pairs of states i and j,
fi'tij' ` fj'tji' (7)
For, if the equality holds in all pairs of states, it must imply that for every transition involving the absorption of photons, a reverse transition will take place involving the radiation of the photon such that there is no net absorption of electromagnetic radiation by the system. This contradicts the original assumption that there is absorption of radiant energy (see previous paragraph), so we must conclude that the equality of forward and reverse transitions do not hold for some pairs of states. However, at steady state, the occupation numbers (or the concentrations of chemical species) are time independent (ie, they remain constant), which means that the sum of all forward transitions is equal to the sum of all backward transitions, ie,
dfi'/ dt = 0 = S (fi'tij' - fj'tji') (8)
But it has already been established that some fi'tij' - fi'tji' are non-zero. That means other pairs must also be non-zero to compensate. In other words, members of the ensemble must leave some states by one path and return by other paths, which constitutes a cycle. Hence, in steady state systems, the flow of energy through the system from a source to a sink will lead to at least one cycle in the system.
The two results - Onsager's reciprocity relationship and Morowitz' theorem of chemical cycles - I believe, imply a third: that symmetrically coupled cycles will arise in open systems which are capable of storing mobilizable energy under energy flow.(7) What are the thermodynamic consequences of symmetrical coupling and cyclic energy relationships?
Let us take cycles first. Cycles return to the same point, and hence the net entropy change is always zero (c.f. Eq. (5) above); and little or no entropy accumulates in the system. These are the relevent non-dissipative processes for which Onsager's reciprocity relationship will apply. More importantly, cycles can be subject to coherent coupling, and that may be why living processes are universally organized over a range of 'biological rhythms'. Coherent coupling, which I shall say more about later, is not why we can move the whole body together, but why we can move different parts independently! Dr. Strangelove - who could not speak without raising his arm - was suffering from a lack of coherent coupling in energy relationships.
Why is symmetrical coupling important? Because it allows energy to delocalize over the whole system as well as to localize to any point, which is ultimately why we can have energy at will, whenever and wherever required. However, to achieve the rapidity with which energy is mobilized in living systems, one requirement is that the energy stores must be distributed over all space-time scales, as it indeed appears to be. For example, skeletal muscles are rich in ATP, whose concentration remains constant, as it is rapidly replaced by creatine phosphate. Before the latter is used up, muscle glycogen breaks down to supply ATP from glycolysis. In the longer term, the lactate accumulating has to be cleared away by the blood supply in exchange for glucose from breaking down glycogen stores in the liver. The various energy stores are themselves replenished progressively starting from very localized substrate oxidation in the mitochondria. Intuitively, one can see that for the most efficient mobilization, the energy stores have to be distributed evenly over all space-time domains, so that every scale can be readily bridged. This is analogous to the problem of percolation in many length and time scales,(17) where large gaps will compromise the transparency of the system.
The organism is indeed vibrant with energy flows on every scale bridging the local and the global, the fast and the slow. Metabolic fluxes are now very actively investigated and evidence is accumulating that the fluxes are dynamically organized in detail down to the molecular level: metabolites are 'channelled' or passed sequentially from one enzyme to the next without being released into the 'bulk aqueous phase'. The cell is thereby partitioned into numerous metabolic 'microcompartments' separating parallel, simultaneous fluxes. A number of different lines of investigation are converging to the conclusion that perhaps no proteins in the cell are dispersed at random in solution, but are instead, organized in an almost solid state. The 'solid' phase also contains a high proportion of the metabolites, and much of the cell water may actually be bound or structured by its enormous amount of surface area.(18) This detailed dynamic organization is optimized thermodynamically, in terms of the efficiency of energy transformation, and kinetically, in terms of the speed with which reactions take place.(8)
These conditions are also very favourable for one of the most neglected energy flows in living systems: electricity and associated electrostatic, electrochemical, dipole and electromagnetic interactions that span all space and time scales from the superfast exchange reactions between contiguous molecules and resonant energy transfers to long-range, global electric and ionic currents and electromagnetic signals between cells and organisms. With characteristic insight and foresight, Szent-Györgi has written 25 years ago,(19)
"..life is driven by nothing else but electrons, by the energy given off by these electrons while cascading down from the high level to which they have been boosted by photons. An electron going around is a little current. What drives life is thus a little electric current."
Welch and Berry (20) argue for "long-range energy continua" connecting all parts of the cell in electrochemical fluxes. In particular, they draw attention to the proton currents (proticity) that may also be flowing, constituting a "protoneural network" that could play a large role in regulating cellular metabolism. Many enzymes, for example, can conduct protons along the hydrogen bonds and/or act as sensors of local electric fields.
The overriding feature of energy mobilization in living systems is that it is stored energy that is being mobilized over all space-time scales, for it is stored energy that is capable of doing work. Stored energy is none other than coherent energy, and the domain of storage is the coherence domain. This immediately suggests that the living system has a full range of coherence times and coherence volumes, the extent of which far exceeds any other physicochemical system.
The energy efficiency of living systems can be adequately accounted for by the thermodynamic considerations I have outlined so far. However, the rapidity and precision with which the energy is mobilized, to my mind, requires additional explanations, and this brings us to coherence defined both classically in terms of phase-transitions, and more rigorously in quantum theory.
An example of phase transition is the Bénard convection cells already mentioned - a phase transition phenomenon in which random molecular movements are transformed into globally coherent flows. Another example is the laser, where energy is pumped into a cavity containing atoms capable of emitting light. As the pumping rate is increased, a threshold is reached - the laser-threshold - at which all the atoms oscillate together in phase, and send out a giant light track that is a million times as long as that emitted by individual atoms. The mathematical theory describing collective phenomena such as the laser (and the Bénard convection cells) is of sufficient generality that it predicts the emergence of global order under very different circumstances. Could something similar be involved in the living organism?
The first detailed suggestion for that was presented by Herbert Fröhlich from the late 1960s to the late 1980s just before he died. Similar ideas had been put forward earlier by Schrödinger (21), Szent-Györgi(19) and Prigogine.(22)
Frohlich(23) argued that as organisms are made up of strongly dipolar molecules packed rather densely together (c.f. the 'solid state' cell), electric and elastic forces will constantly interact. Metabolic pumping will excite macromolecules such as proteins and nucleic acids as well as cellular membranes (which typically have an enormous electric field of some 107V/m across them). The excited molecules/membranes will vibrate at various characteristic frequencies resulting from the coupling of electrical displacements to mechanical deformations. This eventually builds up into collective modes (coherent excitations) of both electromechanical oscillations (phonons, or sound waves in solid medium) and electromagnetic radiations (photons) that extend over macroscopic distances within the organism and perhaps also outside the organism. The emission of electromagnetic radiation from coherent lattice vibrations in a solid-state semi-conductor has recently been experimentally observed for the first time.(24) The possibility arises that organisms may actually use electromagnetic radiations to communicate between cells or between different organisms.(25)
If that is the case, then, as Fröhlich's theory predicts, organisms will be extremely sensitive to weak electromagnetic fields, perhaps through specific coherent excitations, or by interfering with coherent excitations at phase transition. In my laboratory, we have found that brief exposures of early fruitfly embryos to weak static magnetic fields cause characteristic global perturbations to the segmen-tal body pattern of the larvae emerging 24 hours later.(26) As the energies involved are well below thermal threshold, our conclusion was that there can be no effect unless the external field is acting on a coherent domain where charges are moving in phase, or magnetically sensitive dipoles undergoing phase alignment globally.(27)
Although Fröhlich's theory is far from generally accepted, the concept of coherence is already subsumed, or taken for granted, in the description of many macroscopic biological functions, from the synchronous flashing of light among huge populations of fireflies to the coordination of the movements of the four limbs in animal locomotion. In the latter case, each limb has to be treated as a single oscillator with a well-defined collective phase relationship to the other limbs.28 This is an accurate description of what actually happens: each limb moves as one, and not as an unwieldly collection of independent tissues and cells. Similarly, our heart beats as a whole and maintains a phase relationship with our respiratory cycle. Furthermore, as the organs are functioning, the specific groups of nerve cells in the central nervous system connected to the organs will also be firing regularly in unison and exactly in phase with the rhythmic movements of the organs.(29) Let us unravel what is involved here: it is assumed - correctly - that something as complicated as a limb, or a heart, or a whole respiratory system, nevertheless possesses a collective phase of all its multiplicity of activities, i.e., it is coherent. For only when the subsystem is coherent can it couple coherently to other subsystems. This principle extends throughout the organism's space-time domains over which energy is mobilized - each domain being capable of working as an independent coherent unit that is yet in step with the whole. This is where something like quantum coherence has to be invoked, as I shall explain later.
Fröhlich's theory has been extended by a number of theoretical physicists who show that coherent excitations can arise under the most general conditions of energy pumping and energy sharing, and that once established, they are stably maintained.(30) This significant result also invites one to identify an extremum principle for the thermodynamics of open systems which is analogous to that of equilibrium systems.
In working through the bioenergetic relationships of living processes described so far, I came to the conclusion that the following postulates may form the beginnings of a thermodynamics of organized complexity (a slightly different version was presented earlier.(7):
1. Open systems capable of storing energy will evolve to maximize energy storage over all space-time domains, such that the entropy function (analogous to Gibbs entropy),
SG = -Sk pk(r,t) ln pk(r,t) (9)
increases under sustained energy flow.
2. At a certain threshold of energy supply, a phase-transition occurs at which energy mobilization and storage over all space-time domains are coupled together to a single degree of freedom.
3. At phase transition, energy is effectively stored with equal population over all space-time domains, i.e.,
pk(r,t) = constant (S pk(r,t) = 1) (10)
4. This implies that the entropy given in Eq. (9) is both a maximum for the system, but also a minimum at phase transition because the modes are coupled together to a single effective degree of freedom.
The pk(r,t) = constant regime is one of maximum entropy because the potential degrees of freedom are maximized over all space-time domains, but it is also the regime of minimum entropy because the activities in all space-time domains are coupled together so there is only a single actual degree of freedom.(7) Phase transition-like phenomena may be more general than we think. And whenever they occur, something like a maximum-minimum entropy pk(r,t) = constant regime may be involved. Recent work on ant colonies has shown that while individual ants exhibit random behavioural patterns, the collective can undergo phase transition to regular periodic behaviour when the number of ants in the colony reaches a certain threshold. At phase transition, there appears to be a maximum of entropy, measured in terms of the number of active ants per unit period of time, and also a maximum of correlation between ants that are active or inactive.(31) It would be of interest to examine the Fourier spectra at phase transition to see if they too, go through a maximum at phase transition.
The pk(r,t) = constant regime can also be described in terms of the coherent quantum state or 'pure' state consisting of a superposition of many coherent states, so that all possibilities are immediately accessible. The adaptability of the organism depends on just this seemingly paradoxical property. For, only by maximizing the potential degrees of freedom is it possible to access the single degree of freedom that is required for coherent action.(7)
It should be noted that the pk(r,t) = constant regime is a generalization of the discovery made by Fritz Popp from many years of experimentation on light emission from living organisms, which I shall briefly describe below, as it offers further insights into the coherence of organisms.
Although there have been many claims that organisms emit and receive electromagnetic signals in biocommunication, these signals are difficult to detect below the visible range. Fritz Popp is one of the pioneers in detecting ultraweak photon emission from living systems. He and many others since, have found that all organisms emit light ('biophotons') at ultraweak intensities which are strongly correlated with the cell cycle and other functional states.(32) The emitted light typically covers a wide band (200nm to 900nm) around the optical range - the limitation being usually set by the photon-detecting device - with approximately equal numbers of photons throughout the range, for which Popp proposed the
'f (l)=const. rule'.(33)
Biophotons can also be studied as stimulated emission after a brief exposure to light of different spectral compositions. It has been found, without exception, that the stimulated emission decays according to a hyperbolic function; which, according to Popp and Li, is a sufficient condition for a coherent light-field.(34) This implies that photons are held in a coherent form in the organism, and when stimulated, they are emitted coherently, like a very weak, multimode laser. Such a multimode laser has not yet been made artificially, but it is at least not contrary to the theory of coherence in quantum optics as developed especially by Glauber(35), so long as the modes are coupled together.
There is, indeed, evidence that the modes within the visible range are coupled together. Spectral analyses of the stimulated emission show that it always covers the same broad range, regardless of the composition of the light used to induce it, and furthermore, it can retain its spectral distribution even when the system is perturbed to such an extent that the emission intensity changes over several orders of magnitude. Furthermore, the hyperbolic decay kinetics is uniform throughout the spectrum.(36)
Another evidence for the coherence of the photon (energy) field within each organism is that populations of synchronously developing Drosophila embryos can undergo phase-correlated collective light emission minutes to hours after a single brief light stimulation.(37) In order to build up such a phase-correlation, each individual embryo must itself be highly coherent with a definite phase that can phase-lock, or couple coherently, to all the others in the population.(38) That is how the most rapid and effective biocommunication may be achieved in living systems; and we must, finally, consider the important implications of quantum coherence itself.
In order to begin to understand what quantum coherence entails, let us look at Young's two-slit experiment (Fig. 3) in which a source of monochromatic light is placed behind a screen with two narrow slits. As is well-known, light behaves as either particles or waves according as to whether one or both slits are open. When both slits are open, even single photons behave as waves in that they seem to pass through both slits at once, and, falling upon the photographic plate, produces a pattern which indicates that each photon, in effect, interferes with itself! The intensity or brightness of the pattern at each point depends on the sum of four correlation functions:
I = G(t,t) + G (b,b) + G(t,b) + G (b,t) (11)
Fig. 3. Young's two-slit experiment.
where G(t,t) is the intensity with only the top slit opened, G(b,b) the intensity with only the bottom slit opened, and G(t,b)+G(b,t) = 2G(t,b) is the additional intensity (which take on both positive and negative values) when both slits are opened. At different points on the photographic plate, the intensity is
I = G(t,t) + G(b,b) + 2|G(t,b)|cosq (12)
where q is the angle of the phase difference between the two light waves.
The fringe contrast in the interference pattern depends on the magnitude of G(t,b). If this correlation function vanishes, it means that the light beams coming out of t and b are uncorrelated; and if there is no correlation, we say that the light at t and b are incoherent. On the other hand, increase in coherence results in an increase in fringe contrast, i.e., the brightness of the bands. Since cosq is never greater than one (i.e., when the two beams are perfectly in phase), then the fringe contrast is maximized by making G(t,b) as large as possible and that signifies maximum coherence. But there is an upper bound to how large G(t,b) can be. It is given by the Schwarz inequality:
G(t,t,)G(b,b) e |G(t,b)|2
The maximum of G(t,b) is obviously obtained when the two sides are equal:
G(t,t)G(b,b) = |G(t,b)|2 (13)
Now, it is this equation that gives us a description of quantum coherence. A field is coherent at two space-time points, say, t and b, if the above equation is true. Furthermore, we have a coherent field if this equality holds for all space-time points, X1 and X2. This coherence is called first-order coherence because its refers to correlation between two space-time points, and we write it more generally as,
G(1)(X1, X1)G(1)(X2, X2) = |G(1)(X1, X2|2 (14)
The above equation tells us that the correlation between two space-time points in a coherent field factorizes, or decomposes neatly into the self-correlations at the two points separately, and that this factorizability is a sufficient condition for coherence. Factorizability does not mean that the pure state can be factorized into a mixture of states, but it does imply something quite unusual - any two points in a coherent field will behave statistically independently of each other. So two photon detectors in the field will register photons independently of each other.
Coherence can be generalized to arbitrarily higher orders, say, to m approaching , in which case, we shall be talking about a fully coherent field. If mth order coherence holds, then all of the correlation functions which represent joint counting rates for n-fold coincidence experiments (where m<n) factorize as the product of the self-correlations at the individual space-time points. In other words, if we put n different counters in the field, they will each record photons in a way which is statistically independent of all the others with no special tendency towards coincidences, or correlations (see Glauber (35)).
The key to understanding the coherence of organisms is in the factorizability of the quantum coherent state. The coherence of organisms entails a quantum superposition of coherent activities over all space-time domains, each of which correlated with one another and with the whole, and yet independent of the whole. It is this factorizability that underlies the sensitivity of living systems to weak signals, and their ability to communicate and respond with great rapidity. It is why we can attend to all the different vital functions simultaneously and separately, and yet remain an undivided whole.
I have approached the problem of living organization by considering bioenergetic relationships in thermodynamics, where I show how some of the main features of energy mobilization in the living system - its efficiency and rapidity - can be explained by symmetrically coupled, cyclical flows of stored energy over all space-time domains. That is where the possibility for coherence emerges as a critical phase transition, thus connecting with Fröhlich's ideas of coherent excitations and finally, with quantum coherence. The thermodynamical description both leads to, and converges with, the description based on quantum coherence. The living system is maximally efficient, communicative, responsive, and most of all, factorizable, in the sense that the maximum correlation of the local to the global is realized simultaneously with the maximum local freedom. When one ceases to see that as a paradox, one has finally grasped the meaning of organic wholeness or the coherence of organisms.
It is a pleasure to thank Geoffrey Sewell for explaining his generalization of Onsager's reciprocity relationship to me and for many other inspiring comments. I am also grateful to Prof. J. Pokorny for helpful suggestions.
Article first published 1999
Comments are now closed for this article