Time to end the obsession with genes and pay more attention to dynamic processes that generate patterns and forms Dr. Mae-Wan Ho
An impressive army of genes is involved in laying down the body pattern of organisms during early development, and the fruit fly Drosophila is the archetypal example [1, 2]. The genes are expressed in an otherwise featureless embryo, forming remarkable patterns that establish the anterior-posterior body axis and anticipate the subdivision of the body into segments that appear much later in development. The major pathways of gene interactions necessary for determining body pattern in Drosophila were discovered, and Nobel prizes awarded, long before genome sequences were available. Since then, the genomes of some 800 organisms including Drosophila have been sequenced [3], and the gene interactions are being elaborated to the finest detail based on available genomics information [2].
But do we really understand pattern formation in development? I would say no. It remains the greatest unsolved mystery in science.
The project to sequence the human and other genomes has failed to deliver here as in the promises to identify the genes for all our human diseases, failings, and talents (see [4] Ten years of the Human Genome, SiS 48).
Many of the genes involved in pattern determination in Drosophila turn out to have closely similar counterparts in higher animals including the human species. While this may impress some people, others are asking why closely similar genes should give such widely different body patterns. And in any case, the similarity has been exaggerated. For even within the Arthropod phylum, which includes insects like Drosophila, groups differ substantially in the way they form segments and in the genes expressed [5].
There is no doubt that knocking out or mutating genes can interfere with pattern formation, but there is nothing in the action of genes that generate patterns. It is obvious that the genes are responding to and reflecting hidden dynamic processes generating the patterns [6, 7] (Development and Evolution, Development and Evolution Revisited, I-SIS scientific publications), beginning with the initial symmetry-breaking that establishes the major body axis; and these processes deserve attention at least as much as genes. It is time to end the slavish obsession with genes as the answer to everything, and see them as one toolkit among many in the study of living organisms. Fortunately, some scientists have been doing just that.
Patterns are generated everywhere in the physical world where no genes are involved, and many of the patterns closely resemble those found in the living world. It is the dynamics of physical and chemical forces and flows that generate patterns and forms, much as Scottish biologist and mathematician D’Arcy Thompson (1829-1902) so beautifully argued in his classic book, On Growth and Form, first published in 1917 [8]. Closer to our time, Alan Turing (1912-1954), English mathematician, logician, code breaker and computer pioneer, is also well-known for his work on morphogenesis. Turing’s reaction-diffusion model published in 1952 [9] showed, for the first time, how patterns can arise spontaneously in an initially homogeneous domain, precisely the problem of how patterns can form in a featureless egg in development [5, 9-11].
The Turing model inspired much work on pattern formation in biological systems before the human genome project got underway, and it was obscured in the proliferating thicket of genes said to ‘control pattern formation’.
Lately, there has been a Turing revival in developmental biology, as scientists despair of trying to explain pattern formation with complicated computational networks of genes that pass for ‘systems biology’. Shigeru Kondo and Takashi Miura at Osaka University in Japan are part of this movement back to Turing, using a combination of experiments, modelling, and computer simulation.
In a review article, Kondo and Miura stated why they did not concentrate on computational networks of genes [12], because “the behaviour of such systems often defies immediate or intuitive understanding.” And, “it becomes almost impossible to make a meaningful prediction.”
The Turing model on the other hand can explain how spatial patterns can arise “autonomously”, and in nearly limitless variety; not only major body axes, segments and other repeated structures, but also intricate markings on seashells, and exotic pigmentation patterns of fish (see Figure 1).
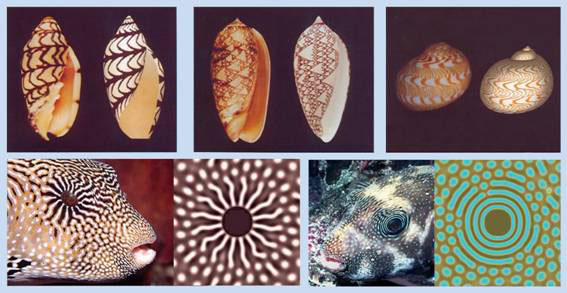
Figure 1 Turing markings on seashells and pigmentation patterns on popper fish; computer generated patterns on right, biological specimen on left of each frame
Moreover it can also explain, if not predict, why experimental manipulations result in very specific novel regenerated patterns. In Figure 2, the zebra fish dark pigment stripes were cut out with a laser. Instead of replacing the original pattern, a new, unexpected pattern was regenerated after 23 days. This was simulated on computer according to a Turing model (bottom of Fig. 2) in which black and yellow pigment cells activated each other at short range while yellow pigment cells inhibited the black pigment cells at long range.
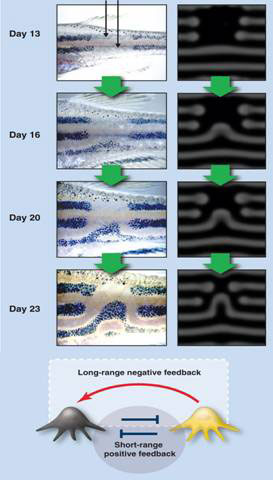
Figure 2 Turing model explains novel regenerated pigment pattern in the zebra fish
Short-range activation and long range inhibition is a necessary condition for pattern formation in Turing’s reaction diffusion model, an important result derived by Alfred Gierer and Hans Meinhardt in the 1970s [13].
Although Turing’s original model involved reaction and diffusion, it has become clear that the model is independent of mechanisms. Any mechanism that produces short range activation and long range inhibition would do just as well [12, 14].
The overriding significance of the Turing model, and indeed a more general mathematical theorem of symmetry-breaking, is that the system, whether physical or biological, spontaneously breaks or reduces existing symmetry [15]. For example, a spherical featureless blob with an infinite number of axes of symmetry can become polarised to radial symmetry. Should it elongate, it loses radial symmetry to become bilaterally symmetric, and so on.
A symmetrical system can lose its symmetry if an asymmetrical state has a lower energy. The initial symmetrical state can be unstable or metastable. An external trigger can push the system from its symmetrical to its asymmetrical state, but simple noise can accomplish the same thing.
Symmetry breaking in biology invariably involves active dynamical processes. Turing showed that patterns can be generated by simple chemical reactions if the reactants have different diffusion rates.
Cells can polarize in response to external signals, such as chemical gradients, cell-cell contacts, and electromagnetic fields. However, cells can also polarize spontaneously in the absence of external influence from internal dynamical processes.
For example, spontaneous polarization can be driven by a mechanical instability of the actin-myosin cortex (layer just beneath the cell membrane) of cells. The cortical actin network is a thin shell of cross-linked actin filaments, myosin motors, and actin-binding proteins between100 nm and1 mm thick, and supports the plasma membrane. The myosin motors generate contractile forces resulting in tensile stress in the actin network. (A stress is force per unit area whereas tension is force per unit length). The tension in the cortex is roughly equal to the stress multiplied by the thickness of the cortex. The elastic energy stored in the stress actin shell can be released by rupture of the network or by the membrane detaching from the cortex, as seen in fibroblasts and lymphoblasts. The relaxed region produces cortical flows or membrane protrusions called blebs.
Flows of the actin-myosin cortex take place in various cell lines at the onset of cell division, which presumably contribute to the cleavage furrow where the daughter cells separate. In some cells, polarization by cortex relaxation may precede cell migration.
Among the first signs of symmetry-breaking in development is an electrical polarization of the egg cell membrane, and a flow of ionic currents through the cell and into the surrounding medium. This may well be universal to all developing systems (see [6]).
The unfertilized eggs of the brown alga Fucus are released into the seawater as uniform spherical cells. The point of sperm entry potentially breaks this symmetry, but the fertilized egg can still be repolarized spontaneously or by environmental stimuli, such as exposure to light in one direction. Fertilization triggers events that break the initial symmetry. Within some minutes, transcellular ion currents can be detected, with Ca2+ entering the pole that will become the rhizoid (root), circulating around the cell, and leaving at the opposite thallus (shoot) pole, thus closing the loop [16]. Associated with this pattern of ionic current is a calcium ion gradient - high at the pole of Ca2+ entry and low at the opposite pole [17] - and an electric field, which is depolarized (less negative) at the pole of Ca2+ entry. So how does this pattern arise spontaneously?
Fabrice Homblé at Free University of Brussels in Belgium, and Marc Léonetti at University of Aix-Marseille in France proposed that the pattern arises from the dynamics of ion conduction through membrane channels – the voltage-dependent calcium channels and a potassium leak – and outside the membrane, diffusion of slower calcium ions relative to potassium.
Sperm entry triggers rapid membrane depolarization and ion channel activation in less than 0.1 ms. Before fertilization, the electric membrane potential difference is about -50 mV. Fertilization by sperm instantaneously gives rise to a fertilization potential, which consists of a fast membrane depolarization from -50 mV to -10 mV, followed by a slow recovery that lasts several minutes. The membrane depolarization provides a rapid electrical block to polyspermy (fertilization by more than one sperm) in the absence of a cell wall.
Membrane depolarization activates both calcium and potassium channels and gives rise to a calcium influx (negative current) and a potassium efflux (positive current). As unfertilized fucoid eggs are excitable, an action potential is triggered when the plasma membrane is depolarized below a threshold (usually at 10 mV more positive than the resting potential). The action potential consists of a transient depolarizing wave lasting ~100 ms with a minimum of -10 mV. The depolarizing phase is due to activation of the voltage-dependent Ca2+ channels, giving rise to Ca2+ influx; the repolarizing phase arises from the activation of the voltage-dependent K+ channels, which let K+ out. This action potential occurs in the presence of voltage-dependent ion channels with nonlinear current-voltage characteristics and when the net conductance of the plasma membrane due to influx of Ca2+ and efflux of K+ (Gca + GK) is negative (<0), because GCa is negative and greater in magnitude than GK. This is the situation in unfertilized focus eggs.
At fertilization, an influx of Na+ probably initiates the membrane depolarization, which triggers the activation of voltage-dependent Ca2+ channels, leading to Ca2+ influx and the amplification of the depolarizing phase. The long-lasting recovery period following is accompanied by an increase of both membrane conductance and K+ permeability. Thus, after fertilization, GK is larger than GCa, and (GCa+GK) >0. This not only blocks polyspermy, but is an essential condition for the formation of stationary spatial patterns of transcellular currents around the zygote. The crucial additional factor is that Ca2+ diffusion is significantly slower than K+. The process is explained in Figure 3.
Starting from a uniform distribution of ion channels and ion concentrations, a local membrane depolarization (dV > 0) gives rise to a Ca2+ influx and a K+ efflux (Fig. 3a). A positive net charge is set up on the cytoplasmic side and a negative one outside giving rise to a lateral electric field (E). K+ flows outside and Ca2+ inside along their electrochemical potential gradient (Fig. 3b). Because K+ diffuse faster than Ca2+, a lateral charge separation (d-, d+) and an electrical potential difference (DE diffusion) is established that amplifies and widens the initial membrane depolarization. This phenomenon will spread along the membrane as channels are progressively activated. Outside the self-organizing (self-amplified) region, the ion electrochemical potential gradients will be dissipated through the membrane forming transcellular current loops. The time constant of this process is given by R2/DCa, where R is the cell radius and DCa is the effective diffusion coefficient of calcium ions.
In Figure 3c, a global picture of the egg is presented. (i) The local perturbation (purple) consists of a depolarization (red inside the cell) surrounded by a hyperpolarization (blue inside the cell) so that the global electric neutrality is preserved. (ii) As the electrical perturbation spreads over the surface, both the central depolarization (red) and peripheral hyperpolarization (blue) zones of the membrane grow, with the central depolarization pushing out the surrounding hyperpolarization. (iii) At the end of the process, a steady state is established where the depolarized area covers half of the zygote surface; while the other half becomes the hyperpolarized area. The red arrow indicates the direction of the electric field inside the zygote, from relatively positive to relatively negative.
Thus, symmetry breaking occurs in some 102 seconds, in agreement with experimental findings that a single but still labile stationary pattern of transcellular currents is established within 30 minutes after fertilization. Membrane, cell wall and cytoplasm reorganization and actin polymerization are essential to sustain, orient and fix the pattern (which is presumably further stabilized by other genes that become expressed).
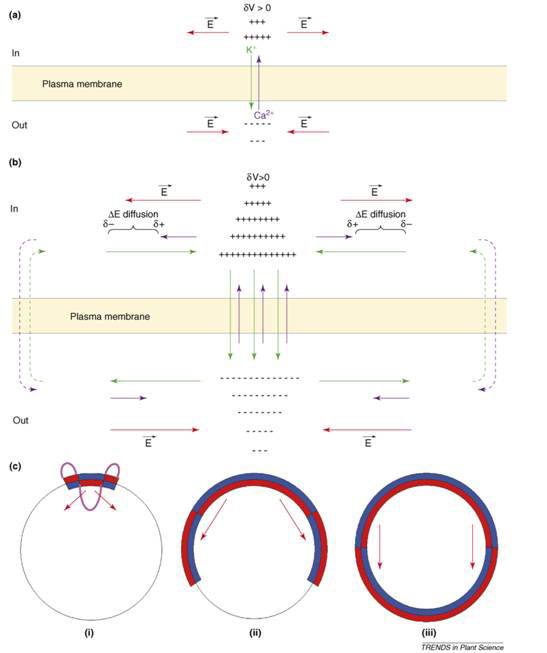
Figure 3 Symmetry breaking in Fucus egg after fertilization and establishment of transcellular ionic current (see text) [16]
The process of establishing transcellular currents and the electric field in the Fucus egg is another example of the Turing model involving local activation (amplification of depolarization) and long range inhibition (hyperpolarization), but the mechanism is electrodynamics, not passive diffusion.
Transcellular currents are associated with spore germination and directional growth and in symmetry breaking in many other plant systems and animal systems, where membrane potential changes are found to determine anterior-posterior axis in development and regeneration, as well as cell proliferation, differentiation and cancer (see [18] Membrane Potential Rules, SiS 52).
These findings highlight the electrodynamical nature of pattern formation in living systems, which are liquid crystalline through and through (see [19] The Rainbow and the Worm, The Physics of Organisms, I-SIS publication). Living liquid crystals are dielectric and intimately associated with water dipoles, and hence particularly prone to electrodynamical patterning, which I shall deal with in the next article [20] (Liquid Crystalline Morphogenetic Field, SiS 52).
Article first published 28/09/11
Comments are now closed for this article