Golden Mean Wins Chemistry Nobel Prize

Quasicrystal structure based on the golden mean won Daniel Shechtman the 2011 Nobel Prize in Chemistry; Dr. Mae-Wan Ho finds out why it is a thing of beauty

Daniel Shectman with quasicrystal icosahedron

Dan Shechtman looked down the electron microscope on the morning of 8 April 1982 and saw the crystal structure of an aluminium and manganese alloy (Al₆Mn) that he had created. It was impossible! He could not believe the structure could exist. A later diffraction pattern obtained with a larger crystal under X-ray showed concentric circles, each with ten bright dots that were equidistant from its neighbours (Figure 1) [1, 2]. He had rapidly chilled the molten metal, and expected the sudden change in temperature to have created complete disorder. Instead, there was order of a different kind from any crystal previously known to exist. He had created a new kind of ordered structure called a quasicrystal.  But it took quite a while for the scientific community to accept his finding.

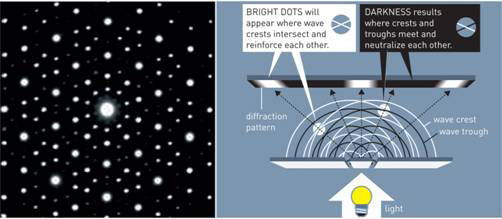
Figure 1   Diffraction pattern of Dan Shechtman’s crystal (left) and how it was obtained

“I told everyone who was ready to listen that I had material with pentagonal symmetry. People just laughed at me,”  Shechtman recalls when interviewed in his office at the Israel Institute of Technology, Haifa, Israel, surrounded by numerous prizes he has won before the crowning glory of the Nobel award [3].

In fact, Shectman lost his job soon after his discovery. Linus Pauling accused him of “talking nonsense”, and delivered the ultimate insult [4]: “There is no such thing as quasicrystals, only quasiscientists.”

Quasicrystals a new kind of solids

A quasicrystal is an ordered structure that is not periodic. It can continuously fill all available space, but it lacks translational symmetry, which means that an arbitrary part of it cannot be shifted from its original position to another place without destroying the symmetry. While crystals, according to the classical ‘crystallographic restriction theorem’, can possess only two, three, four, and six-fold symmetries, quasicrystals show other symmetry orders, for instance five-fold.

Paul J. Steinhardt, professor of physics at Princeton University, New Jersey, in the United States defines quasicrytals more precisely as quasiperiodic structures with forbidden symmetry that can be reduced to a finite number of repeating units [2]. These structures were inspired by Penrose tilings in two dimensions.

Aperiodic tilings were discovered by mathematicians in the early 1960s. In 1972, Roger Penrose created a two-dimensional tiling pattern with only two different pieces that was not periodic and had a five-fold symmetry (see Figure 2).

Figure 2  Penrose tilings from John Steinhardt with 5, 7 and 11-fold symmetries (left to right) [2]

Quasicrystals are higher dimensions Penrose tiling (and obey rules other than what Penrose had discovered).  They are a new class of solids not just with 5-fold symmetry, but any symmetry in any number of dimensions [2]. This includes a dynamic icosahedron quasicrystal structure of 280 molecules of water discovered by Martin Chaplin at South Bank University, London, in the UK [5, 6] (see Two-States Water Explains All? SiS 32).

Quasicrystals and the golden mean

An intriguing feature of quasicrystals is that the mathematical ‘irrational’ constant (irrational because it cannot be expressed as a fraction) known as the Greek letter j, or the “golden ratio” is embedded in the structure [5, 7], which in turn underlies a number sequence worked out by Fibonacci in the 13th century, where each number is the sum of the preceding two.

Two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is approximately 1.61803398874989. Other names frequently used for the golden ratio are the golden proportion, the golden section, or golden mean.

The Fibonacci sequence is a sequence of numbers, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ….., where the ratio of a number in the sequence to the previous approaches j  asymptotically, i.e., more and more exactly as the numbers get larger and larger.

The golden mean was the Greek ideal of beauty and harmony, and had a tremendous influence on architecture, art and design.

It is significant that quasicrystals do represent minimum energy structures [2, 5], and hence a kind of frozen equilibrium between harmony and tension in just the right degree, which may be where beauty lies.

Article first published 07/11/11

---

References

1. “Crystals of golden proportions”, Ann Fernholm, The Nobel Prize in Chemistry 2011, The Swedish Academy of Sciences.
2. Steinhardt PJ. What are quasicrystals?, www.physics.princeton.edu/~steinh/QuasiIntro.ppt
3. “Clear as crystal”, Asaf Shtull-Trauring, 22 October 2011, HAARETZ.com,  http://www.haaretz.com/weekend/magazine/clear-as-crystal-1.353504
4. Dan Shechtman discusses quasicrystals, ScienceBase, Shectman video interview, David Bradley, 5 October 2011, http://www.sciencebase.com/science-blog/dan-shechtman-discusses-quasicrystals-nobelprize.html.
5. Platonic solids, Water structure and science, Martin Chaplin, accessed 23 October 2011, http://www.lsbu.ac.uk/water/platonic.html
6. Ho MW. Two-states water explains all? Science in Society 32, 17-18, 2006.
7. Some solids (three-dimensional) geometrical facts about the golden section. Gionacci numbers and the golden section, Ron Knotts,  accessed 23 October 2011, http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/Fibonacci/phi3DGeom.html