I-SIS mini-series New Age of Water
The age-old mystery of water is unfolding as a recent model of a large hydrogen-bonded water superstructure matches practically all observations. Dr. Mae-Wan Ho
Water is the most abundant substance on earth, and life as we know it is impossible without water. There are very few molecules simpler than water, yet its behaviour is most complex and unusual. As chemist-natural theologian Lawrence J Henderson pointed out at length in his book The Fitness of the Environment published in 1913 [1], the strangeness of water consists of precisely the properties that make water ‘fit’ for life on earth .
Compared to its neighbours in the Periodic Table of chemical compounds, water is definitely out of line (see Table 1). Hydrides (compounds with hydrogen) in the first row are all gases at ambient temperatures (above 20C), and except for HF, boiling well below 0 C, the freezing point of water. As one moves up column for Group 6a hydrides from Te (tellurium) to S (sulphur), their boiling points progressively decrease. Extrapolating these boiling points to the molecular weight of water gives an expected boiling point of about –75 C instead of 100 C. Water should be a gas at ordinary temperatures and pressure, and not a liquid.
Table 1. Water stands out from its neighbours
Group |
3a |
4a |
5a |
6a |
7a |
B2H6 -92.5 |
CH4 -164.0 |
NH3 -33.4 |
H2O +100. 0 |
HF +19.5 |
|
H2S -60.7 |
|||||
H2Se -41.5 |
|||||
H2Te -2.0 |
The strangeness of water is a consequence of the extensive three-dimensional hydrogen bonding of water molecules to one another, which is what makes water a liquid rather than a gas at ordinary temperatures and pressure; breaking those bonds requires an abnormally high temperature. The hydrogen bonds in water are much stronger than those in NH 3 and HF, which is why the latter have much lower boiling points.
As a liquid, water behaves contrary to ordinary liquids. For example, water frozen into solid ice floats in the liquid, and the volume occupied by the ice contracts when it melts to liquid. That means liquid water is denser than its solid phase, which is the opposite of what happens when other liquids turn into solids, they become more dense as the molecules are more restricted in motion and packed closer together.
Liquid water can be super-cooled (cooled below its freezing point without freezing); but on heating, the super-cooled liquid does not expand as expected. Instead it shrinks until a maximum density is reached at about 4 C. Under pressure, both the melting point and the maximum density point shift to lower temperatures. With ordinary liquids, pressure promotes freezing and consequently shifts the freezing point to higher temperatures.
The compressibility of water declines with increasing temperature, reaching a minimum near 46.5 C, whereas warmer liquids are usually more compressible. At sufficiently high pressures, the anomalous volume and temperature behaviour disappears.
Another surprise is that at ordinary temperatures below 35 C, increasing the pressure results in lower viscosity, again the opposite of what happens in other liquids [2].
These strange properties of water have intrigued generations of scientists who have tried to explain them. Wilhelm Conrad Röntgen, who discovered X-rays and was awarded the Nobel Price in Physics in 1901, was also the first to suggest that liquid water exists in two states, bulky (low-density) and high-density [3].
The mixed two-states model of water has been revived by a number of scientists in recent years, especially as structural studies on solid ice and super-cooled water have yielded good data. There are at least 13 known forms of ice, depending on pressure and temperature [4] (Is Water Special), so the idea that there may be at least two states of water does not seem unreasonable.
The late Wilse Robinson and his group in Texas Tech University Lubbock in the United States revived the two-states theory of water in the 1980s. By the early 1990s, they were able to show that the experimental measurements of the density of water over the range of -30 C in the super-cooled region to 70 C could be accurately fitted to the two-states model [2]. They envisaged low-density regions in the liquid with intermolecular hydrogen bonds like that of ordinary ice Ih intermixed with high-density regions with compact bonding similar to ice II. As temperature approaches 225 K (-48 C) in the deep super-cooled regime, only ice 1 type bonding is present.
X-ray diffraction data on liquid water, and other structural data on different forms of ice indicated that high-density and low-density water (HDW and LDW) differ in bonding in larger water structures.
At ordinary temperatures, liquid water consists of rapidly inter-converting LDW clusters where the second neighbour intermolecular O---O distance is 0.45 nm, and compact, HDW clusters where the corresponding O---O distance is 0.35 nm. In super-cooled water, LDW clusters predominate, and hence its volume shrinks when heated, as more and more HDW clusters form until 4 C, when practically all the clusters are HDW, and the water is at its maximum density [5].
The X-ray scattering data contain a lot of information, especially in the radial distribution function that gives the probability of finding a second molecule at a distance r from a first. When the probabilities are plotted against r , a series of peaks and troughs appear, including one at 0.35 nm (second-neighbour O---O distance of HDW), which has never been adequately explained on a structural basis.
The two-states network model of Robinson and colleagues leaves some questions unanswered. For instance, considerable pressure would be required for the extensive formation of ice II clusters (from ice Ih) to get the density of water right and the required number of non-bonded close contacts between water molecules.
While the molecular movements in liquid water require constant breaking and reorganization of individual hydrogen bonds on a picosecond (10 -12 s) time scale, it is thought that at any instant, the degree of hydrogen bonding is very high, greater than 95 percent.
Martin Chaplin at Southbank University in London, UK, was impressed at the many pieces of evidence pointing towards a large extent of order in the hydrogen-bonded network of water molecules. These include the fine structure in the X-ray diffraction data, vibration spectra that indicate the presence of large clusters and the formation and properties of low-density water in gels (Water and Effortless Action at a Distance , this series). A random network has been described for LDW and super-cooled water, but the entropy (a measure of disorder) of LDW is much lower than that of a random network.
Although several workers including Robinson have suggested that the structure of liquid water should be related to ice forms (see above), the structures in liquid water must be significantly different from ice, because water super-cools quite easily, and releases a high heat of fusion when it freezes, indicating a large loss of energy.
In an ingenious feat of molecular modelling, Chaplin proposed that the fluctuating network of molecules in liquid water is organized locally into an iscosahedron (many-sided three-dimensional hexagonal shapes made of many small triangles) consisting of 280 fully hydrogen-bonded molecules . Each iscosahedron is formed by the regular arrangement of 20 identical units of 14 water molecules [6].
The icosahedron structure explains many anomalies of water including its temperature-density and pressure-viscosity behaviour, its radial distribution function, the presence of pentamers and hexamers of water molecules, the change in properties and the ‘two-states’ model on super-cooling.
Further on, it also explains the interactions of ions, hydrophobic molecules, carbohydrates and macromolecules with water [7] ( The Importance of Cell Water).
Chaplin developed the model by assembling alternating sheets of boat-form and chair-form water hexamers from the lattices of hexagonal and cubic ice respectively using the software package Hyperchem. The resulting icosahedron contains 280 water molecules all except for those in the outer ring, completely hydrogen-bonded, two as donors and two as acceptors. It has large pores capable of partial collapse due to interactions between hydrogen-bonded partners competing with interactions between non-hydrogen bonded neighbours. It also has cavities capable of enclosing small solutes.
The 280-molecule icosahedron measures 3 nm in diameter in its fully expanded form. The beauty of the model is that it can convert between a low-density fully expanded structure (ES) and a high-density collapsed structure (CS) without hydrogen bonds breaking; they only need to bend (Fig. 1), with bond strengths about one percent smaller in CS.
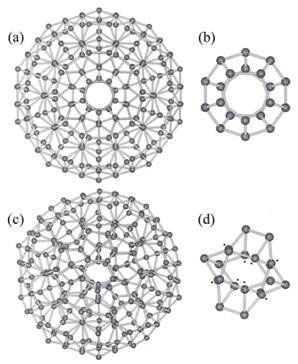
Figure 1. Chaplin’s two-states model of highly ordered icosahedral network that interconverts between the fully expanded low-density form (a) and the collapsed high-density form (c); with their respective central 20 molecules (dodecahedral) units (b) and (d) (from ref. 6)
Chaplin’s model explains an impressive list of observations . The density of ES is 0.94 g cm-3 and that of CS, 1.00 g cm-3 . The density of ES is comparable to that of low-density water at 0.96 g cm-3 found around macromolecules, and that of super-cooled water (-45 C) and low-density amorphous (noncrystalline) ice, both at 0.94 g cm-3 . The density of CS on the other hand, compares with that of water at 0 C, also 1.00 g cm-3 . CS is capable of further collapse with weaker hydrogen bonding or greater pressure. Collapse of all dodecahedron structures gives a density of 1.18 g cm-3 similar to the density of 1.17 g cm-3 of high-density amorphous ice.
The strongest evidence for Chaplin’s model is the agreement with the radial distribution function. The CS model was used to generate a radial distribution function of the intermolecular O---O distances and compared with that from X-ray data at 4 C. The peaks are in the same positions, albeit less distinct in the X-ray data because of the relative movements expected in a real liquid. There are 16 peaks plus a further 34 blips using the first derivative (change of probability with r), which make a total of 50 positions. All 50 positions except for two show correspondence between the X-ray data and those predicted from CS. There is also good correspondence with the radial distribution function derived from neutron diffraction data, although those show less fine structure than X-ray.
Support for the structure of ES comes from its agreement with radial distribution functions of solutions, super-cooled water and low-density amorphous ice. The cavity-cavity peak at 0.55 nm of super-cooled water is close to the cavity-cavity peak predicted from ES at 0.54 nm.
Since Chaplin proposed his model, the inner four shells of ES (Fig. 1), consisting of 160 water molecules (20 H2O at 0.39 nm; 20 H2O at 0.66 nm; 60 H2O at 0.79 nm; 60 H2O at 1.06 nm) have been found in almost identical positions and orientations within a nanodrop of water encapsulated in polyoxomolybdate [8].
“The evidence for my model has accumulated since, and there is no counter-evidence.” Chaplin says. But he cautions against the idea that the icosahedron structures are permanent or even complete. “The molecules are in constant flux but the structuring remains. Consider the similarity with a wave at sea where the structure of the wave continues across an ocean but the water molecules come and go.”
Chaplin’s model may turn out to account also for many astonishing properties of water in dilute solutions, such as water crystals with unit cells measuring hundreds of nanometres in dimension (Colloid Crystals , this issue) and the possibly, the massive exclusion zones (hundreds of microns deep) formed on the surfaces of gels and rabbit muscle, which contain no dissolved solutes [9] ( Water Forms Massive Exclusion Zones). Watch this space .
Article first published 25/10/06
Comments are now closed for this article