To tackle urbanization, the most pressing problem of this century, theoretical physicist Geoffrey West is on a quest for a grand unified theory of sustainability based on universal scaling in biology and cities Dr. Mae-Wan Ho
Urbanization has been expanding rapidly within the past 200 years; emerging as the most pressing global problem of this century. Since the year 2006, those of us who live in cities have exceeded 50 % of the world population. Today, more than 80 % of people in developed countries such as the United States are urbanized, and by 2050, more than 75 % of the world population will live in cities.
Geoffrey West, theoretical physicist and distinguished professor at Santa Fe Institute in the United States, summed up the challenges of urbanization in his public lecture [1]: “Cities are the origins of global warming, impact on the environment, health, pollution, disease, finance, economies, energy – they’re all problems that are confronted by having cities.” On the other hand, he also noted that cities have proven to be [2] “engines of creativity”, wealth creation and economic growth.
He called for [1, 3] a “Grand Unified Theory of Sustainability.”
It has been long recognized that cities can save energy on mass and food transport, and facilitate the provision of essential services for health, education, sanitation, and energy, as well as building communities [4]. The idea of sustainable cities goes back at least to the 1980s. For example, Richard Register coined the term ecocity in his book [5] Ecocity Berkeley: Building Cities for a Healthy Future. Architect Paul F. Downton, founded the company Ecopolis in 1990, specializing in ecological architecture and bio-urban design [6] and published a book on the subject in 2009 [7].
There is no agreed definition for a sustainable city. Nevertheless, the following would probably be generally acceptable: a sustainable city should be able to feed and power itself using land and energy efficiently with the least environmental pollution and impact on climate change, minimizing waste, and recycling and reconverting wastes into resources. A long list of sustainable or ecocities are found in countries across the world [4], with indicators for sustainability typically in three areas – economy, environment and social – the details depending on local conditions [8]. There is strong emphasis on green spaces, renewal energies/energy efficiencies, reduced carbon emissions, transport, water availability and quality, air quality, and minimising and recycling waste for the environment; complete neighbourhood, equity and affordable housing as well as education, sanitation and health for the social; and employment rates especially in green jobs, and economic growth for the economy. Surprisingly there is nothing on food and its availability, considering that 842 million people worldwide do not have enough to eat [9].
Since the 1990s, stimulated by the science and mathematics of complex system, there has been substantial effort dedicated to understanding cities in terms of fractal geometry and dynamics [10]. Fractals are geometrical or mathematical objects with fractional dimensions instead of the usual integer 1, 2, 3, or 4. They also have self-similar properties, i.e., they appear similar on different scales. Siena is a wonderful example of a fractal city (Figure 1).

Figure 1 Fractal city of Siena
Flowing fractal structures are evident in the aerial picture of the city, and on a smaller scale, the self-similar constructions in the façade of the Siena Cathedral, and smaller yet, the beautiful cathedral-like arches in the polyptych of the Madonna and Child and the Saints by Duccio. Obviously, the architects and artists had a deep intuitive understanding of complex mathematics and its aesthetics 800 years ago.
Fractals are also the key to living organization and characteristic of living organisms, and this led to the transition in thinking of cities as machines to cities as organisms [11]. While living cities have fractal properties that extend downwards to human scales, these are lacking or destroyed in modernist cities built for the automobile and population growth. These fractal properties are being recreated and recovered [12] for example in pedestrian walkways and precincts such as those along and across the River Thames in London [13]. A related move is ‘smart growth’ [14] in urban planning to avoid urban sprawl. It advocates compact, transit-oriented walkable, bicycle-friendly land use, with neighbourhood schools, complete streets that include safe access for bicycles, pedestrians as well as for delivering goods, and mixed-use development that blends a combination of residential, commercial, cultural, institutional or industrial uses with a range of housing choices, all aimed at restoring connectivity and structures on human scales. Much attention is obviously being paid to the social aspects of sustainability.
Despite these promising developments, cities are still poorly understood; there is as yet no real science of cities [10], let alone a grand unified theory of sustainability [1, 3]. Nevertheless there are hints that a theory of sustainable cities may exist, and fractals very much part of it.
West made his reputation in a team that produced the first overarching theory of allometric scaling in biology [15-17], which I have referred to enthusiastically as [18] Biology’s Theory of Everything (SiS 21). Allometric scaling is the observation that physiological parameters such as resting metabolic rate tend to scale with body mass
Y = AXb (1)
where both A and b are constants. Plotting log Y against log X gives a straight line with slope b and intercept log A. The value of b is ¾, and this applies from mouse to elephant and even from bacteria to whales and giant redwood trees over 21 orders of magnitude in body mass. While basal metabolic rates of entire organisms scale as X3/4, rates of cellular metabolism, heartbeat, embryonic growth and life-span scale as X1/4.
The theory presented by West and colleagues is based on fractal networks. Living organisms are maintained by the transport of materials through fractal networks such as the blood vessels in vertebrates, the trachea in insects and the xylem and phloem (branching tubes transporting water and nutrients) in plants. These branching fractal structures are optimised for transport, maximising the area across which they can take up and release resources and minimising the energy needed to deliver those resources through the organism. In other words, they accomplish their task most efficiently with the least dissipation of energy. These networks are space-filling in three dimensions, but not quite three dimensional, and hence have a fractional dimension between 2 and 3. They are similar over many scales, as characteristic of fractals. The sublinear scaling (b < 1) indicates that there is economy of scale, doubling the size of the organism does not require double the energy, but only 75 % more. In other words, the bigger the organism, the more relatively efficiently they are at using energy, at least viewed from the outside.
I have conjectured that the fractal networks are coherent structures [18], in keeping with the quantum coherence of organisms that approaches zero entropy production suggested by other empirical evidence and theoretical considerations presented in my book [19] The Rainbow and the Worm - The Physics of Organisms (ISIS publication). Since then, Giuseppe Vitiello, theoretical physicist at University of Salerno, Italy, has provided an important proof that fractal structures are mathematically isomorphic with squeezed quantum coherent states (in which Heisenberg’s uncertainty is minimum) [20]. Quantum coherence also dovetails with the circular thermodynamics of organisms with minimum entropy production (minimum dissipation) that I have perfected in successive editions of the Rainbow Worm [19] and applies well to cities, as I shall show later [21] (Sustainable Cities as Organisms, SiS 64).
Do cities have characteristics of organisms? Do they show universal scaling like organisms? Yes they do. Cities also have networks for transport of goods and people, for supply of energy and for intercommunication. But according to West and his colleagues especially Luis Bettencourt [2], the most important network is people. Cities too, scale sublinearly with size (expressed as number of people) for infrastructure such as the number of petrol stations, length of roads, electrical lines, etc. There is economy of scale by about 15 % (see Figure 2A) [22]. There are similar savings in carbon footprints; Bettencourt claims most large developed cities are greener than average in terms of per capita carbon emission.
More surprisingly cities also scale superlinearly, by approximately the same amount (Fig. 2B) in gross domestic product, wages, income, creativity (number of patents), employment, and unfortunately, also in crime, traffic congestion, disease, debt, pollution, etc. Superlinear scaling, says West, never happens in biology [1, 3].
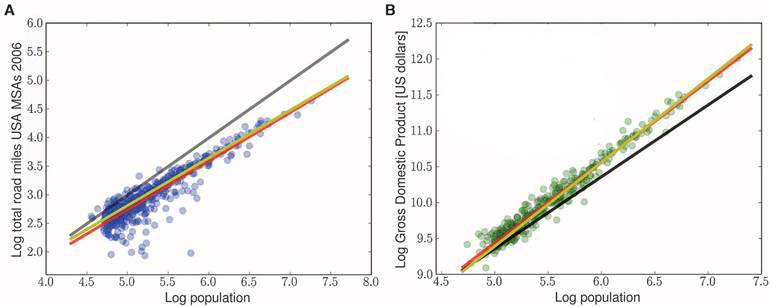
Figure 2 Sublinear and superlinear scaling in cities (see text for details)
Actually, superlinear scaling or hyperallometry (as opposed to hypoallometry or sublinear scaling) is quite well-known in animal and plant morphology, and furthermore is flexible and changeable according to environmental conditions [23]. Incidentally, cerebral grey matter apparently scales superlinearly with an exponent of 5/4, as West himself previously pointed out [24].
To explain the fundamental distinction made between cities and organisms, West states [1, 13] that organisms grow ‘sigmoidally’ (i.e., logistically), which means exponentially at first then slow down and stop when mature; whereas cities never stop growing exponentially, and ‘the pace of life’ becomes faster and faster until a final ‘collapse’. West further suggested that cities maintain that exponential growth and avoid collapse through major innovations, which have to happen faster and faster.
There is little or no evidence that cities grow exponentially especially in developed countries, which supply all the data so far. (If they do, that is a sure sign of unsustainability!) There may be much more evidence that cities too, grow logistically like natural populations in general, as enshrined in Alfred Lotka’s law of population growth [25].
Bettencourt [22] offers a more elaborate mathematical theory based on social networks among the city’s inhabitants and incorporating fractal geometry. The theory predicts that infrastructure scales as 1 - d ≃ 5/6 whereas social interactions scale as 1 + d ≃ 7/6 where d= H/[D(D+H)] ≃ 1/6, with H the fractal dimension taken as 1, and D the ordinary dimension 2. This model fits with observations of sublinear scaling for infrastructure in US and German road networks and tracks the average built area of more than 3 600 large cities worldwide measured through remote sensing (Fig.2A). The social interaction scaling of 1 + d ≃ 7/6 was observed in urban telecommunication networks, and presumably applies to other superlinearly scaled parameters (Fig. 2B).
Further elaboration of the model takes into account the cost of maintaining the city connected as the energy necessary for moving people, goods and information across its infrastructure networks, and energy dissipation W, which scales superlinearly with exponent 1+d ≃ 7/6. Thus, energy dissipation scales with population like social interactions, as was observed in German urban power grids. The ratio Y/W, a measure of urban efficiency where Y is social interaction outcome, is assumed to be independent of city size.
Bettencourt then identifies a quantity L, net urban output , as the difference between social interaction outcome Y and infrastructure energy dissipation W, and predicts an optimal connectivity G* at dL/dG = 0 [22] (Figure 3A and B), and an expectation that values of G among cities fluctuate around G* (Figure 3C).
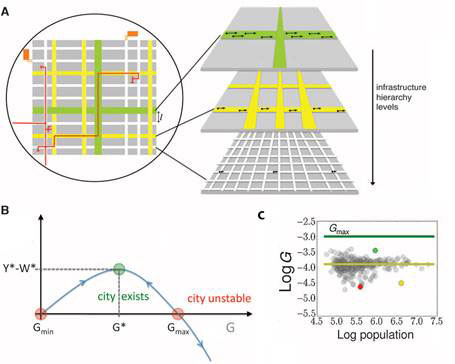
Figure 3 Fractal geometry of infrastructure network for social interactions (A) net social output versus connectivity (B) and log G vs log population for cities in Figure 2 (C)
The limiting values of G follow from the solutions to L= 0: G=0 and G= Gmax. Thus, cities will form if the balance of social interactions is positive. However, there is an upper value of G = Gmax beyond which dissipation costs overcome social benefits and a city may split into regions (this is perhaps a more realistic scenario than the cataclysmic ‘collapse’ envisaged by West). For G < G*, the social interaction potential of a city is underdeveloped. Such places tend to be poorer and have less advanced infrastructure. Thus, cities such as Riverside, California (yellow circle, Fig 3C) or Brownsville, Texas (red circle, Fig.3C) would benefit from measures that promote greater mobility or density for more intense and beneficial city-wide social contact. Conversely, cities with G>G* become victims of their socioeconomic success by incurring escalating mobility costs; Bridgeport Connecticut (green circle, Fig. 3C) being an example, and might generally benefit from increases in transportation energy efficiency. Cities may be suboptimal either because they do not realize their full social potential or because they do so in a manner that renders transportation costs too high.
The scaling of cities that West, Bettencourt and colleagues discovered is very important, and does point the way to a science of cities. However, for reasons already mentioned, I do not find West or Bettencourt’s theory of cities convincing. The distinction drawn between organisms and cities based on superlinear scaling in cities but not organisms is false; and there is little or no evidence that cities grow exponentially as opposed to organisms and natural populations (including humans) which grow logistically. Thus, cities may be more like organisms rather than being distinctly different from them.
Bettencourt’s model is to some extent produced to fit the ‘universal’ scaling exponents observed. ‘Universal’ does not imply ‘invariant’; In fact, there is quite a spread in the observed range of the exponents listed in Table 1 of his paper [22]. Bettencourt’s energy dissipation W scaling superlinearly with size depends on people mixing to the same extent in small and in large cities, which is unrealistic. The degree of mixing depends on neighbourhoods in a fractal way, we tend to see our immediate neighbours more often than those living in the next street and much more often than those living in the next borough, and so on.
A new scaling study using more detailed data and a rational clustering method for identifying cities found a strong superlinear scaling exponent of 1.46 of CO2 emissions with population [26] (see also [27] Large Cities in USA Less Green than Small Ones, SiS 64). It shows convincingly that large cities emit proportionately more CO2 per capita than small ones. This contradicts previous findings by Bettencourt and colleagues of sublinear scaling for CO2 emissions and the claim that large cities are greener than small ones [22].
The studies on cities so far indicate that cities may not be so different from organisms, but they are by no means sustainable on the whole. In other words, they may be more like sick organisms than healthy ones. And there are readily available remedies.
Energy dissipation for transport is a critical factor in making cities sustainable and therefore more like healthy organisms. Not only does the amount of energy dissipation depend on distance, it also depends on the means of transport, the means of energy generation, the nature of the grid providing the energy, and whether energy is generated, used and stored locally. For example, city buses powered by biogas (from anaerobic digestion of municipal wastes), or electric trains or cars drawing power from solar/wind/hydro renewable sources, and a flexible distributed grid with plenty of local energy storage could reduce dissipation to a minimum. Germany is transforming its electricity grid along with local energy storage to take full advantage of its distributed renewable energy generation capacities (see [28] Renewable Ousting Fossil Energy, SiS 60). This could make entire countries as well as cities more like an organism, in which energy is produced for local use and stored locally, but also ready to be deployed anywhere it is needed [19]. Similarly, restoring fractal properties to large cities by creating local communities and pedestrian precincts and adopting smart growth for cities (see earlier) would cut down on the need for dissipative transport and at the same time benefit the local economy.
Better still, green organic spaces, tree-lined boulevards, parks, organic urban and peri-urban food production, as already practiced in cities all over the world, green roofs, green residences, green offices, all would help absorb and reduce CO2 emissions while regenerating O2, and help provide food and food security at greatly reduced food miles (Figure 4).

Figure 4 Organic green spaces in and around the city (from various sources [29-36])
For organisms, the most robust exponent values appear in the scaling of basal or resting metabolic rate with body size and other physiological variables (16 in all) closely tied to metabolic rate. This extends over 27 orders of magnitude from redwood giants down through cells to mitochondria and the respiratory molecular complex [24], a truly impressive universality. West and his colleague James Brown rightly identified the origin of this universality in thermodynamics, arguing that organisms are thermodynamically optimised for energy transfer and mobilization, but, lacking a thermodynamic theory, they also appealed to Darwinian natural selection in the optimization.
My own conjecture in the second and third editions of the Rainbow Worm in 1998 and 2008 respectively [19] is that the universal scaling depends on the circular thermodynamics (economy) of nature that results in dissipationless (zero entropy) energy transfer and transformation in the ideal, which is also implied in the quantum coherence of organisms.
Core energy metabolism is indeed the realm of thermodynamics, or the economy of nature; and if cities were to be compared to organisms, then it is the transformation of energy and materials – the true thermodynamics or economy of cities - that we need to address, at least in the first instance. Social action taken by human beings can have both positive and negative impacts on the economy of cities (and of nature). Sustainable systems (including economic systems) are like organisms in many respects [37, 38], and sustainable cities may indeed be considered as organisms. Thinking of cities as organisms is in turn a good guide to making cities (and economies) sustainable. That is what I shall be talking about in my Prigogine Medal 2014 Lecture for Sustainable City 2014, 9th International Conference on Urban Regeneration and Sustainability, University of Siena, 23 September 2014 (http://www.wessex.ac.uk/14-conferences/sustainable-city-2014.html).
Article first published 03/09/14
Comments are now closed for this article