Dr. Mae-Wan Ho, Institute of Science in Society. Invited lecture for conference on Environment, Agriculture, Food, Health and Economy, World Food Day, 17 October 2007, La Sapienza University, Rome, Italy
I have developed a “thermodynamics of organized complexity” based on a nested dynamical structure that enables the organism to maintain its organisation and simultaneously achieve non-equilibrium and equilibrium energy transfer at maximum efficiency (Ho 1993, 1998a, 2007a).
The healthy organism excels in maintaining its organisation and keeping away from thermodynamic equilibrium – death by another name – and in reproducing and providing for future generations. In those respects, it is the ideal sustainable system (Ho, 1998b,c; Ho and Ulanowicz, 2005). Looking at sustainable systems as organisms provides fresh insights on sustainability, and offers diagnostic criteria that reflect the system’s health.
This paper formalises and updates the ‘zero-entropy’ model of organisms and sustainable systems, and shows how sustainable development is possible by explicit reference to a ‘zero-emission’, ‘zero-waste’ integrated food and energy ‘Dream Farm 2’.
Key Words: Cycles, coherent energy storage, space-time structure, fractal dynamics, sustainability, sustainable development, minimum entropy production, internal entropy compensation, circular economy
Schrödinger (1944) wrote: “It is by avoiding the rapid decay into the inert state of ‘equilibrium’ that an organism appears so enigmatic…What an organism feeds upon is negative entropy. Or, to put it less paradoxically, the essential thing in metabolism is that the organism succeeds in freeing itself from all the entropy it cannot help producing while alive.”
Schrödinger was struggling to make explicit the intimate relationship between energy and organisation. To make progress, we need to see life with fresh eyes.
By half accident, we discovered in my laboratory in 1992 that all living organisms display dynamic liquid crystalline rainbow colours under the polarising light microscope that geologists use to look at rock crystals and other birefringent materials (Ho and Lawrence 1993; Ho et al, 1996; Ross et al, 1997). The fact that living moving organisms, with all their molecules churning around transforming energy could appear like a dynamic liquid crystal display is evidence that living organisms are coherent (organized) to a high degree, right down to the alignment and motions of the protein molecules in their tissues and cells, and it is coherent energy that is being mobilized and transformed in the organisms (Ho 1993, 1998a, Ho et al, 2006b).
This spurred me on to reformulate thermodynamics for living systems over the past 15 years, the details of which are presented in successive editions of The Rainbow and the Worm, the Physics of Organisms (Ho, 1993, 1998a, 2007a). I shall recapitulate the main results and bring this work up to date, as it has large implications for the environment, food, health and the economy, the themes of our conference.
The first thing to take note is that organisms do not make their living by heat transfer. Instead, they are isothermal systems (c.f. Morowitz, 1968) dependent on the direct transfer of molecular energy, by proteins and other macromolecules acting as “molecular energy machines”. For isothermal processes, the change in Gibbs free energy is,
DG = DH - TDS (1)
Thermodynamic efficiency requires that DS, the change in entropy, approaches 0 (least dissipation), or DG, the change in free energy, approaches 0 (free energy conservation or entropy-enthalpy compensation) (Ho, 1995).
The organism as a whole keeps far away from thermodynamic equilibrium, but how does it free itself from “all the entropy it cannot help producing while alive”? That’s the point of departure for the “thermodynamics of organised complexity”.
The pre-requisite for keeping away from thermodynamic equilibrium – the state of maximum entropy or death by another name – is to be able to capture energy and material from the environment to develop, grow and recreate oneself from moment to moment during one’s life time and also to reproduce and provide for future generations, all part and parcel of sustainability.
The organism has solved its problems of sustainability over billions of years of evolution. It has an obviously nested physical structure. Our body is enclosed and protected by a rather tough skin, but we can exchange energy and material with the outside, as we need to, we eat, breathe and excrete. Within the body, there are organs, tissues and cells, each with a certain degree of autonomy and closure. Within the cells there are numerous intracellular compartments that operate more or less autonomously from the rest of the cell. And within each compartment, there are molecular complexes doing different things: transcribing genes, making proteins and extracting energy from our food, etc. More importantly, the activities in all those compartments, from the microscopic to the macroscopic are perfectly orchestrated, which is why the organism looks like a dynamic liquid crystal display, as explained earlier.
An organism has physical barriers separating the inside from the outside, but never completely. It can be questioned whether such physical closure is necessary, at least as far as the sustainable system is concerned. More important than physical closure is dynamic closure, which enables the organism to store as much energy and material as possible, and to use the energy and material most efficiently, i.e., with the least waste and dissipation (see above).
The key to understanding the thermodynamics of the living system is not so much energy flow (Prigogine, 1967, Morowitz, 1968, and Ulanowicz, 1983) as energy capture and storage under energy flow (Fig. 1). Energy flow is of no consequence unless the energy can be trapped and stored within the system, where it is mobilised to give a self-maintaining, self-reproducing life cycle coupled to the energy flow. (By energy, I include material flow, which enables the energy to be stored and mobilised.)
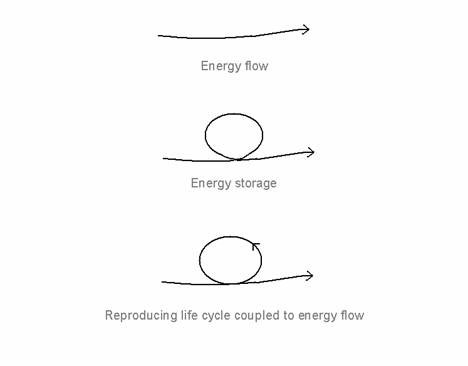
Figure 1. Energy flow, energy storage and the reproducing life-cycle
My approach diverges significantly from the framework established by earlier applications of thermodynamics to ecology as described in detail in Ho and Ulanowicz (2005). Stored energy is distinct from exergy as widely used by ecologists, and also from free energy as defined by chemists and physicists (see Eq. 1). It is stored energy being mobilised in a non-classical steady state that characterise living organisms and sustainable systems, as will be made clear below.
The perfect coordination (organisation) of the organism depends on how the captured energy is mobilised within the organism. It turns out that energy is mobilised in cycles, or more precisely, quasi-limit cycles, which can be thought of as dynamic boxes; and they come in all sizes, from the very fast to the very slow, from the global to the most local.
Cycles provide the dynamic closure that’s absolutely necessary for life, perhaps much more so than physical closure.
Biologists have long puzzled over why biological activities are predominantly rhythmic or cyclic, and much effort has gone into identifying the centre of control, and more recently to identifying master genes that control biological rhythms, to no avail.
The organism is full of cycles, possibly because cycles make thermodynamic sense. (Nevertheless, Morowitz (1968) has proven an important theorem that a flow of energy from a source to a sink in a system at steady state will lead to at least one cycle.) Cycles mean returning again and again to the same states, and no entropy is generated in a perfect cycle. In other words, the system as a whole remains organized. Cycles give dynamic stability as well as autonomy to the organism; and this is apparently also the case in ecosystems (Ulanowicz, 1983). Moreover, cycles enable the activities to be coupled, or linked together, so that those yielding energy can transfer the energy directly to those requiring energy, and the direction can be reversed when the need arises. This is implicit in Onsager’s reciprocity relationship which shows how symmetrical coupling of processes can arise naturally in a system under energy flow (see Ho, 1993, 1998a, 2007a). These symmetrical, reciprocal relationships are most important for sustaining the system. Our metabolism is actually organised precisely in that way: closing cycles and linking up, with pathways that readily reverses the direction of energy and material flows.
Figure 2 is a diagram representing the nested cycles that span all space-time scales, the totality of which make up the life cycle of the organism (Ho, 1998a). The life cycle has a self-similar fractal structure, so if you magnify each cycle, you will see that it has smaller cycles within, looking much the same as the whole. Fractal dynamics are the hallmarks of natural processes and are especially fit for the organisation of living systems (Ho, 2007a), as we shall see.
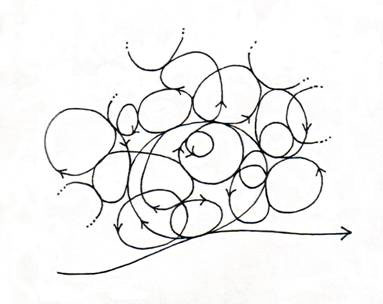
Figure 2. The life cycle of the organism consists of a self-similar fractal structure of cycles turning within cycles
This complex nested dynamical space-time structure of the organism is the secret of sustainability. As explained below, it maximises the efficiency and rapidity of energy mobilisation, and the degree of space-time differentiation is directly correlated with the amount of energy stored.
Physiologist Colin McClare (1971) made an important contribution towards reformulating thermodynamics so that it can apply to living systems. He proposed that in a system defined by some macroscopic parameter, such as temperature, q, its energies can be separated into two categories: stored (coherent) energies that remain in a non-equilibrium state within a characteristic time, t, and thermal (random) energies that exchange with each other and reach equilibrium (or equilibrate) in a time less than t (see Fig 3).
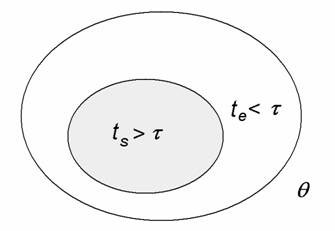
Figure 3. Stored vs thermal energy
McClare introduced time structure into systems, with the very important consequence that there are now two ways to mobilise energy efficiently with entropy change approaching zero: very slowly with respect to t, so it is reversible at every point; or very rapidly with respect to t, so that the energy remains stored as it is mobilised.
For a process with characteristic timescale of 10-10s, a millisecond is an eternity, so a ‘slow’ process need not be very slow at all to be energy efficient. Most enzyme reactions therefore could be occurring at thermodynamic equilibrium. On the other hand, resonant energy transfer is an example of a very fast process occurring in <10-14s, so the energy remains stored as it is transferred. The latter process too, is very important for living systems. Resonance interactions coordinate reactions in different parts of the cell and the organism. Resonating molecules attract one another, and there is indeed recent evidence that proteins, nucleic acids and other molecules find one another through resonating to the same electromagnetic frequencies (see Ho, 2007b).
McClare (1971) proposed that, “Useful work is only done by a molecular system when one form of stored energy is converted into another”. In other words, thermalised energies cannot be used to do work, and thermalised energy cannot be converted into stored energy. This raised obvious objections, as critics pointed out, automobiles do run on thermalised energy from burning petrol, so the proposal could not be right.
McClare’s proposal was incomplete, and I completed his proposal as follows (Ho 1993, 1995): “Useful work is only done by a molecular system when one form of stored energy is converted into another in the same system.” The additional phrase “in the same system” effectively defines a ‘system’ by the extent to which thermal energies equilibrate within a characteristic space-time.
In the case of the automobile and other similar contraptions, the hot gases expand against a constraint, the piston, which, in taking up the thermalized energy, does work against the system external to the combustion chamber.
This definition of a system is crucial for the nested space-time structure of the organism. The organism is actually partitioned into a hierarchy of systems within systems within systems defined by equilibration space-times. Energies thermalised or equilibrated within a smaller space-time (system) will still be out of equilibrium in the larger system encompassing the first (see Fig. 4). So, even though the organism as a whole is far from thermodynamic equilibrium, its space-time differentiation nevertheless allows for a hierarchy of local near-equilibrium regimes to be maintained within.
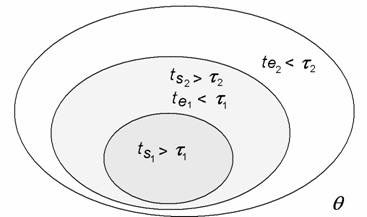
Figure 4. A nested hierarchy of space-times in which equilibrium and non-equilibrium co-exist
Stored energy, like exergy and free energy, refers to energy available for doing useful work. But stored energy is explicitly defined with respect to a characteristic space-time, and is hence a real property of systems rather than a pseudo-property (see Ho and Ulanowicz, 2005).
The nested space-time structure in organisms optimises thermodynamic efficiency by allowing the organism to simultaneously exploit equilibrium (very slow) and non-equilibrium (very fast) energy transfers with minimum dissipation, always with reference to the characteristic timescales of the processes involved as described above. It also optimises the rapidity of energy mobilisation. Biochemical reactions depend strictly on local concentrations of reactants, which could be enormously high, depending on their extent of equilibration, which is generally quite restricted. Cell biologists are beginning to take seriously the view that the cell approaches the solid-state, or more accurately, a liquid crystalline state, where nothing is freely diffusible, and even the cell water is organized into polarized multi-layers (Ho, 1998a, 2007a, Ho et al, 2006b; see also Ling, 2001).
Another point to note is that the greater the space-time differentiation, the more coherent energy is stored within the system. Because the activities are all coupled together, the energy residence time depends on how many activities there are within the system.
Finally, there is a dynamic structure to the space-time differentiation, so the activities can remain mostly distinct and independent, and yet are poised to exchange energies with one another. In other words, the energies in different space-time domains need to be separately mobilised and yet able to spread from any point to the entire system, and conversely, converge from all over the system to any point whenever and wherever required. I have proposed that a self-similar fractal organisation provides such a space-time structure (Ho, 1998a, b, c). But it was only a few days ago that I suddenly realised why.
As we were about to watch Simon McBurney’s A Disappearing Number at the Barbican, a play created around the Indian mathematical sensation Srinivasa Ramanujan, I asked Peter Saunders if all irrational numbers were arbitrarily close to rational numbers, and he said yes. My guess was that because all fractals are close to harmonics (or in mathematical terms, every irrational number is arbitrarily close to a rational number), phase coupling and energy transfer through resonance is readily achieved by shifting from fractals to harmonics. There is now abundant evidence that fractal dynamics characterizes the healthy heart rhythm, which reflects the constant intercommunication between the heart and all other parts of the body (see Ho, 2007c). Real time monitoring also shows how the heart rhythm can change abruptly, and how positive emotions such as love and appreciation can make the heart beat in synchrony with the pulse and respiratory rhythms, possibly through resonance on a macroscopic scale (see Ho 2007d).
In the ideal – represented by the healthy mature organism as well as the healthy mature ecosystem (Odum, 1969) - the system is always tending towards a dynamic balance, a non-classical steady state (Fig. 5), as will be explained shortly. The simple equation, S DS = 0, inside the cycle, says there is an overall internal conservation of energy and compensation of entropy so that the system organisation is maintained and dissipation minimized (Schrödinger’s negentropy); while the necessary dissipation exported to the outside, is also minimised, S DS > 0.
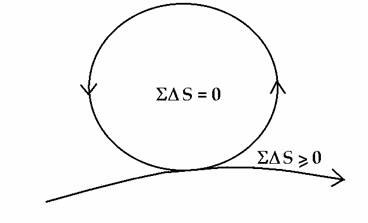
Figure 5. Zero-entropy model of the ideal organism and sustainable system
Internal entropy compensation and energy conservation implies that positive entropy generated somewhere is compensated by negative entropy elsewhere within the organism over a finite time. This is possible only if the internal microscopic detailed balance at every point of classical steady state theory is violated.
Denbigh (1951) defined the steady state as one in which “the macroscopic parameters such as temperature, pressure and composition, have time-independent values at every point of the system, despite the occurrence of a dissipative process.” That is far too restrictive to apply to the organism and the sustainable system. Instead, Ho (1993, 1998a) proposed to define the living system in homeostasis as a “dynamic equilibrium in which the macroscopic parameters, such as temperature, pressure and composition have time-independent values despite the occurrence of dissipative processes.” The omission of the phrase “at every point of the system” is significant.
Microscopic homogeneity is not necessary for the formulation of any thermodynamic state, as the thermodynamic parameters are macroscopic entities quite independent of the microscopic interpretations. Like the principle of microscopic reversibility, it is extraneous to the phenomenological laws of thermodynamics, as Denbigh himself had convincingly argued.
It is the organised space-time heterogeneity within the living system that allows for the necessary ‘free’ variation of the microscopic states within the macroscopic thermodynamic constraints. Thus, stability criteria that apply to the system as a whole need not be satisfied, or stronger yet, cannot be satisfied in every individual space-time element for all times.
The tendency to conserve coherent energy and compensate for entropy production within the system will result in the minimum entropy being exported to the outside. Intuitively, one can see that if the system were maximally efficient, then it would also produce the least dissipation.
From the outside, it might appear that the system is “maximally dissipative” in terms of having “degraded” the energy gradient most effectively (Schneider and Kay, 1994; Hannon and Ulanowicz, 1987). But this misses the coherent energy stored non-degraded within the system, and stored energy is also embodied in biomass.
I have suggested diagnostic criteria of sustainability or health that depend on the tendency of a sustainable system to maximize non-dissipative cyclic flows of energy and minimizing dissipative flows (Ho, 1998c).
Maximising non-dissipative cyclic flows will increase the following: energy storage capacity, which translates into carrying capacity or biomass; the number of cycles in the system; the efficiency of energy use; space-time differentiation, which translates into biodiversity; balanced flows of resources and energy; reciprocal coupling of processes. The minimization of dissipation will result in reducing entropy production (towards zero).
These diagnostic criteria are interlinked, so once one is identified, the others are likely to follow. Some support for these criteria is that they are similar to those Schneider and Kay (1994) have identified for mature, established ecosystems (Ho, 1998c). Data collected for carbon-energy flows in two aquatic marsh ecosystems next to a large power-generating facility in the Crystal River in Florida showed that the ‘stressed’ system, exposed to hot water coming out of the nuclear power station, which increased the temperature by 6 C, captured 20% less energy, made 20% less efficient use of the energy captured, had 50% fewer cycles and 34% less biomass than the control.
Schneider and Kay (1994) also drew attention to some interesting measurements made by Luvall and Holbo (1991) with a NASA thermal infrared multispectral scanner from the air, which assess energy budgets of terrestrial landscapes. They found that the more developed the ecosystem, the colder its surface temperature. This is consistent with the maximisation of energy storage capacity and the minimisation of dissipation.
Another indication of the energy efficiency and potential increase in carrying capacity of sustainable systems is provided by a comparison of 25 rice cultivation system (see Ho 1998c), of which 8 were pre-industrial in terms of low fossil fuel input (2-4%) and high labour input (35-78%), 10 were semi-industrial with moderate to high fossil fuel input (23-93%) and low to moderate labour input (4-46%) and seven were full industrial with 95% fossil fuel input and extremely low labour input of 0.04 –0.2%). The total output per hectare (in GigaJoule) in the pre-industrial fell into a low (2.4 to 9.9) and a high-output (149.3 to 166.9) subgroup, with the former one-twentieth to one-fifth of the full industrial average. However, the output of the high subgroup was two to three times the full-industrial systems. The yields of semi-industrial systems were more homogeneous, with an average of 51.75GJ, while the yields of full-industrial systems, even more uniform, averaged 65.66 GJ.
When the ratio of total energetic output to total input was calculated, the pre-industrial low yielding systems ranged between 6.9 and 11.5, whiles figures for the high output system registered from 15.3 to 29.2. Semi-industrial systems gave ratios of 2.1 to 9.7, whereas the ratios of full-industrial systems were not much better than unity. These figures illustrate the law of diminishing returns: there seems to be a plateau of output per hectare around 70-80 GJ regardless of the total input, which is only exceeded in the three high-yielding pre-industrial systems of Yunnan, China. Intensifying energy input led to a drop in efficiency, particularly sharp as input approaches the output ceiling, which appeared to conform to the notion of a uniform carrying capacity. But this is highly misleading, as the carrying capacity depends on how the land is organised for production (see below).
There is no longer any doubt that we are living through climate change as fossil fuels are fast depleting, and hurricanes, droughts and floods are destroying lives, homes and crops all over the world. I remain optimistic, however, because we actually have a wealth of knowledge that is capable of provide food security and health for all, and significantly mitigate climate change (Ho et al 2006a).
A major obstacle to implementing this knowledge is the overwhelming commitment of our elected representatives to the dominant neo-liberal economic model, otherwise known as the environmental bubble-economy (Brown, 2003). It is based on the exploitation of environmental resources beyond their capacity for renewal or regeneration in order to fuel perpetual economic growth.
I have proposed a ‘zero-emission’, ‘zero-waste’ ‘Dream Farm 2’ based on the zero-entropy model. In practice, Dream Farm 2 maximises the use of renewable energies and turns ‘wastes’ into food and energy resources, thereby freeing us completely from fossil fuels (for the latest update see Ho, 2007e) (Figure 6).
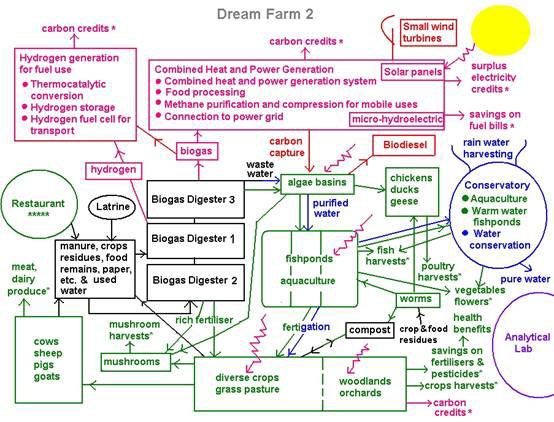
Figure 6. Dream Farm 2 based on the zero-entropy model of the organism
The diagram is colour-coded: red is for energy, green for food, black is waste in the conventional sense of the word, but is soon transformed into resources, and blue is for water conservation and flood control, a key requirement in stable food and energy production under the vagaries of rainfall patterns now experienced across the world.
The anaerobic digester is the core technology for treating wastes, preventing pollution and generating energy. Livestock manure, food, paper and other biological remains are fermented by naturally occurring waste-gobbling bacteria and turned into biogas, which provides much of the energy needs. The partially cleansed wastewater goes into the algal basins where algae photosynthesis produces all the oxygen needed to detoxify the water, making it safe for the fish. The algae are harvested to feed chickens, ducks, geese and other livestock. The fishponds support a compatible mixture of 5-6 fish species. Water from the fishponds ‘fertigates’ crops growing in the fields or on the raised dykes. Fruits and vegetables can be grown in floats on the surface of the fishponds. Water from the fishponds can also be pumped into greenhouses for aquaculture of fruits and vegetables. The water, purified of nutrients, is returned to the aquifers. The anaerobic digester yields a residue rich in nutrients that is an excellent fertiliser for crops. It can also be mixed with algae and crop residues for culturing mushrooms after steam sterilisation. The residue from mushroom culture can be fed to livestock or composted. Crop residues are fed back to livestock. Crop and food residues can be used to raise earthworms to feed fish and fowl. Compost and worm castings go to condition the soil. Livestock manure goes back into the anaerobic digester, thus closing the grand cycle. The result is a highly productive farm that’s more than self-sufficient in food and energy, and saves substantially on carbon emissions.
Anaerobic digestion of livestock and other wastes saves carbon emissions twice over, by preventing the serious greenhouse gases methane and nitrous oxide from reaching the atmosphere, and by methane substituting for fossil fuel use to run vehicles and farm machinery. For a country like the UK, anaerobic digestion of all biological wastes could provide more than 11 percent of the country’s energy use and more than 50 percent of its transport fuels.
In addition, all the building materials will be sourced, and buildings designed to minimise carbon emissions and energy use.
The farm will incorporate other forms of renewable energies suitable for local energy generation at the medium, small to micro-scale: solar panels/walls, small wind turbines, and microhydroelectric generators where appropriate.
The approach is to get the farm up and running while new technologies and designs are researched and incorporated, such as generating hydrogen from wastes or from methane, using algae to capture carbon dioxide from combined heat and power generation and making biodiesel, and fuel cells that take methane to reform into hydrogen. All of that will be part of an education/research component of the farm. The farm will also provide an excellent showcase for new, appropriate technologies.
Dream Farm 2 illustrates how the zero entropy model contrasts with the dominant model, and more importantly, how it is possible to have sustainable growth and development. Too many critics of the dominant paradigm think that the only alternative to unsustainable growth is to have no growth at all.
The minimum entropy exported to the environment is important, as the system depends on environmental input, hence, entropy exported to the environment will simply mean diminished environmental input. This can be made more explicit by enclosing the system within the immediate environment of the system as in Figure 7.
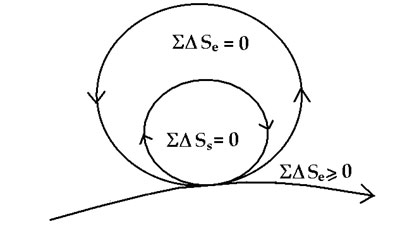
Figure 7. The coupled flows of system and ecological cycles in a sustainable system
The ecological environment surrounding the system is now explicitly represented also as a zero-entropy cycle. You have to imagine, once again, that this is a fractal diagram, and that the environment surrounding the system is itself exporting to a larger ecological domain, and this kind of embedding can go on, ultimately to the entire earth. And of course, each cycle is made up of many smaller cycles within (see Fig. 2) all working by reciprocity and cooperation.
In contrast, the dominant model of infinite competitive growth is a case of the bigger fish swallowing the smaller ad infinitum, and it describes equally how a person should behave and how a company should develop in order to be successful. But it is the entropy and waste generation that concerns us here, so I have represented it diagrammatically in Figure 8. This system grows relentlessly, swallowing up the earth’s resources, laying waste to everything in its path, like a hurricane. There is no closed cycle to hold resources within, to build up stable organised social or ecological structures. It captures the essence of our ‘boom and bust’ economy. The money market is especially entropic, as I have pointed out elsewhere (Ho 1998b, c), mainly because it is not based on any real-valued goods or services; furthermore, it artificially inflates the purchasing power of the rich, leading to greater exploitation of environmental resources.
Figure 8. The dominant economic model of infinite unsustainable growth that swallows up the earth’s resources and exports massive amounts of wastes and entropy (left) contrasted with the zero-entropy model
The dynamically closed cycle of the zero-entropy mode, on the other hand, enables stable organised social or ecological structures to build up, and to grow and develop in a balanced way, as distinct from the dominant model of infinite, unsustainable growth.
As in the zero-entropy model of the organism, the sustainable system’s cycle contains more cycles within that are interlinked symmetrically to help one another thrive and prosper (see Fig. 2). This principle is well illustrated in sustainable integrated farming.
The minimum integrated farm has the farmer, livestock and crops (Fig. 9). The farmer prepares the ground to sow the seeds for the crops to grow that feed the livestock and the farmer; the livestock returns manure to feed the crops. Very little is wasted or exported to the environment. In fact, a high proportion of the resources are recycled and kept inside the system. The system stores energy as well as material resources such as carbon. The extra carbon is sequestered in the soil as the soil improves, and in the standing biomass of crops and livestock.
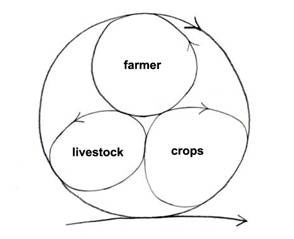
Figure 9. The minimum integrated sustainable farm
More importantly, the farm can perpetuate itself like that quite successfully and sustainably, or it can grow by engaging more cycles, units of devolved autonomy that help one another do better. (In analogy with the organism, it will develop a more complex space-time differentiation, and grow bigger.)
In the old paradigm, organisms are predominantly seen to compete for resources and for space. But we’ve got three space dimensions and the time dimension too. We’ve got space-time that we can fill up more thickly with life cycles of different sizes that occupy different space-times. That is exactly what organisms in a naturally biodiverse ecosystem do to maximise the reciprocal, symbiotic relationships that benefit all the species. So you can add fish, algae, poultry, worms, mushrooms, etc., turning the ‘waste’ from one cycle to resource for another (Fig.10).
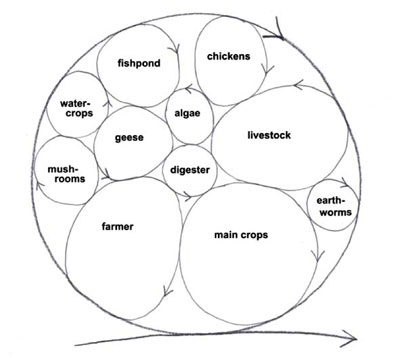
Figure 10. Sustainable system develops and grows by incorporating more life cycles within the system, the wastes from one cycle is resource for another.
The more lifecycles incorporated, the more energy and standing biomass are stored within the system, and the greater the productivity of the farm. It will also support an increasing number of farmers and farm workers.
Productivity and biodiversity always go together in a sustainable system, as generations of farmers have known, and recent academic researchers have rediscovered. I had predicted the same earlier on the basis of a space-time differentiation that maximises distributed energy storage (Ho, 1998b,c). The different life cycles are essentially holding the energy for the whole system, and by way of reciprocity, recycling the energy within the system. Once it is recognized that coherent energy is stored within the system, it follows that energy can be recycled, contrary to the conventional wisdom that regards only materials as capable of being recycled.
Industrial monoculture, in contrast, is the least energy efficient in terms of output per unit of input, and often less productive in absolute terms despite high external inputs (see above), because it does not close the cycle, it does not have the biodiversity (space-time differentiation) and reciprocity to hold the energy within and ends up generating a lot of waste and entropy and depleting the soil.
In a recent visit to China, I was delighted to discover that something very similar to the model of sustainable systems as organisms is in the official Chinese mainstream discourse; they call it the “circular economy”. Chinese farmers have perfected it over the past two thousand years especially in the Pearl River Delta of southeast China (Ho 2006). It disposes of another myth: that there is a constant carrying capacity for a given piece of land, in terms of the number of people it can support.
There is a world of difference between industrial monoculture and circular integrated farming, it is the difference between the dominant linear input-output maximum entropy model and the zero-entropy sustainable model. The carrying capacity depends on how the land is organised for production. The Pearl River Delta sustained an average of 17 people per hectare in the 1980s, a carrying capacity at least ten times the average of industrial farming, and two to three times the world average.
The thermodynamics of organisms and sustainable systems tells us not only why we must move away from the dominant environmental bubble economy, but especially how we can create a healthier, richer, more equitable and satisfying life without fossil fuels, and we should start right now.
I am very grateful to Mario and Loredana Pianesi of Un Punto Macrobiotico for inviting me to this conference and instigating this paper.
Peter Saunders is used to having questions on mathematics fired at him at random. This time it was a direct hit, and the excitement has yet to subside.
Article first published 21/09/07
Comments are now closed for this article