Science of the Organism
From chaotic dynamics of natural processes to sublime music and information processing in the brain. Dr. Mae-Wan Ho

What could possibly connect cascading sand-piles, avalanches, music, brainwaves and more? It is ‘self-organized criticality’, described in a paper published in 1987 co-authored by theoretical physicist Per Bak (1948-2002) [1]. Self-organized criticality is a property of dynamical systems that look the same on different scales, hence referred to as self-similar, or scale-invariant [2]. It is to be found at the critical point of a phase transition, as when water turns to ice, or a ferromagnet becomes fully magnetized.
Self-organized criticality is also a way of understanding complex systems in nature. It stems from the discovery that complexity could be generated as an emergent (new and unexpected) feature of extended systems from simple local interactions, for example, in work on cellular automata by Polish mathematician Stanislaw Ulam (1909-1984) and Hungarian-American mathematician John von Neumann (1903-1957), plus a large body of work on fractal geometry – self-similar mathematical structures - by Polish-born French mathematician BenoÎt Mendelbrot (1924-2010). Meanwhile, extensive investigations on phase transitions in the 1960s and 1970s showed how scale-invariant fractals and power laws emerge at the critical point. A power law is a mathematical relationship often referred to as the 1/f law (after the 1/f electronic noise of transistors) in which the distribution of power density at different frequencies (power spectral density) is inversely proportion to the frequency, i.e.,
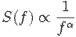 (1)
(1)
where f is the frequency and a an exponent generally between 0 and 2. Note that f can be any quantity, not just noise or frequency of the electronic signal. It could apply to size, or amplitude, or duration (of time).
Per Bak, Chao Tang and Kurt Wiesenfeld put all those ideas together in their paper [1]. They used the analogy of a pile of sand at the point of collapse, when the avalanches take on all sizes from small to large, but are distributed according to the 1/f power law, so that frequency of avalanches at different sizes scale as the inverse of size: small ones are more frequent than medium and medium more frequent than really big ones. A log-log plot of frequency vs size results in a straight one, the slope of which gives the exponent.
The key result of the Bak-Tang-Wiesenfeld paper was to demonstrate how the complexity observed emerges spontaneously in a robust way that does not require any fine tuning or regulation, like the collapse of a sand pile under gravity at the point when it is piled high and big enough.
However, that is only part of the story of complex systems, and to this day, researchers are debating whether the 1/f power law is really applicable to natural phenomena, and what exactly it implies about the underlying mechanisms.
Before venturing further, let’s see what the 1/f distribution can tell us about music.
Why do we love music? One reason we enjoy music lies in its balance of predictability and surprise, so researchers claim. They found musical pitch (frequency) spectrum following a 1/f power law, which achieves this balance of predictability and surprise; but what about musical rhythm? Musical rhythms, especially those of Western classical music, are highly regular and predictable; are they? Daniel Levitin at McGilll University Canada, Parag Chordia at Georgia Institute of Technology Atlanta and Vinod Menon at Stanford University California in the United States decided to put that to the test by analysing the rhythm spectra in 1 788 movements from 558 compositions of Western classical music [3].
The rhythmic content of the compositions were systematically measured by noting the durations of the notes and of the rests, transforming the durations into Hz (cycle per second), plotting the data and finding the spectral exponent in the slope of the line obtained. They went through the works of 40 composers in 16 subgenres, and found an overwhelming majority of rhythms following the 1/fa power law with a ranging from ~0.5 to ~1. An exponent of 0 would be pure white noise, completely unpredictable, whereas an exponent of 2 and above would be highly predictable. Notably, classical composers whose compositions are known to exhibit nearly identical 1/f pitch spectra demonstrated distinctive 1/f rhythm spectra: Beethoven’s rhythms were among the most predictable, and Mozart’s among the least, with Haydn in between (Figure 1). The difference in rhythmic predictability is such as to allow composers to identify their compositions uniquely and to distinguish them from works of their contemporaries.
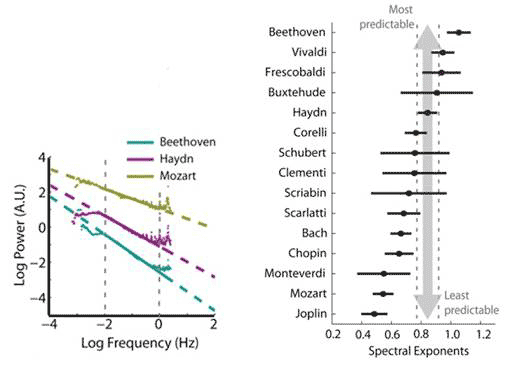
Figure 1 Power spectra and exponents of rhythms in Western classical compositions by composers
Previous studies analysing classical compositions from the 18th to 20th century reported nearly identical 1/f pitch structure among composers, with a very narrow range of spectral exponent 1.79-1.97. In contrast, the rhythm spectral exponent varied widely and systematically among composers from 0.48 to 1.05. Even composers belonging to the same musical classical era – Beethoven, Haydn and Mozart - demonstrated distinctive rhythm spectra.
Time structure in classical music turns out to be much more nuanced than previously suspected. This is of great interest to me, as this whole enquiry around the golden ratio began because I wanted to find out how it might be involved in the space-time structure of organisms, i.e. organic quantum space-time (as opposed to mechanical clock time of the Newtonian universe). Organic space-time has been a major theme of [4] The Rainbow and the Worm, The Physics of Organisms (ISIS publication) since its first 1993 edition. I surmised that organic space-time is fractal, as French astrophysicist Laurent Nottale has proposed that relativistic-quantum space-time is fractal [5].
Organic space-time is organized as cycles of activity (or oscillations) over many scales [4], generally recognized as the all-pervasive biological rhythms ranging from split seconds to days and years that have preoccupied physiologists and ecologists alike at least since the 18th century [6]. The cycles are coupled such that activities yielding energy transfer it directly to those requiring it with minimum loss or dissipation, and the directions can be reversed whenever required [4]. This scale-invariant space-time structure is the key to the efficiency and rapidity of energy transfer within living systems. Energy can be drawn from any local level to the global, and conversely, it can be concentrated to any local domain from the entire system. In the ideal, the system tends towards quantum coherence – an incredibly dynamic ‘quantum jazz’ over all space-times – that maximises both local freedom (autonomy) and global cohesion. How could that be achieved? How could we have local autonomy and be able to transfer energy rapidly from local to global and vice versa?
The only way that could be achieved, I suggested, is that the frequencies of biological rhythms are irrational multiples of one another [7] (Thermodynamics of Organisms and Sustainable Systems, I-SIS Lecture) [8] under steady-state default conditions, perhaps even multiples of the golden ratio. However, the frequencies are close enough to rational multiples, that they can slide towards rational multiples to achieve phase synchrony or phase-locking, thereby enabling energy transfer via resonance or positive interference.
There is no evidence as yet that biological rhythms in general are organised as irrational multiples. However, oscillations in local field potentials in the brain are found to approximate multiples of the most irrational number, the golden ratio, and this appears crucial in how the brain processes information or makes music.
Electrical activities from the surface layers of the brain are readily recorded via an array of sensitive electrodes positioned on the scalp. This procedure, electroencephalography (EEG), records voltage fluctuations in the local fields, or local field potentials (LFPs) around groups of thousands of neurons close to each electrode.
Belinda Pletzer, Hubert Kerschbaum and Wolfgang Klimesch at the University of Salzburg in Germany have recognized the importance of brain frequencies that never synchronize in the resting brain. They reasoned that if the electrical oscillations in the brain are involved in communication between different brain structures and networks, it is important for groups of cells to keep their rhythms distinct without interference from other groups, and without interfering with the rhythms of other groups. And that is indeed achieved via frequencies in irrational multiples in the resting (default) brain [9].
The brain functions in a massively parallel and distributed manner. Which processes are responsible for communication between the largely distributed brain structures? One possibility is oscillations. During the highly excitable phase, neurons are very likely to fire (spike in an action potential), whereas during the low excitability phase, activity is reduced or suppressed. Consequently, the oscillations facilitate simultaneous activation of common target cells and enhanced firing through an assembly of cells, and may be highly important in gating cognitive processes (especially in a quantum coherence brain, see [10] Quantum Coherence and Conscious Experience, I-SIS scientific publication).
It is generally assumed that functional interplay between different cell assemblies is reflected by oscillatory coupling of several different kinds of phase synchrony and phase-locking. However, it is just as important to avoid spurious coupling that interferes with function. Therefore, frequencies in the default resting state should be arranged so that they never synchronize. The best way this could be achieved is to have frequencies in multiples of the most irrational number, the golden ratio (see [11] The Story of Phi, SiS 62). To prove their point, Pletzer and colleagues tabulated the typical EEG frequencies in recordings made mostly when subjects are in a ‘resting’ state, not engaged in any mental processing tasks (Table 1).
Table 1 Typical EEG frequency bands and subbands and corresponding periods
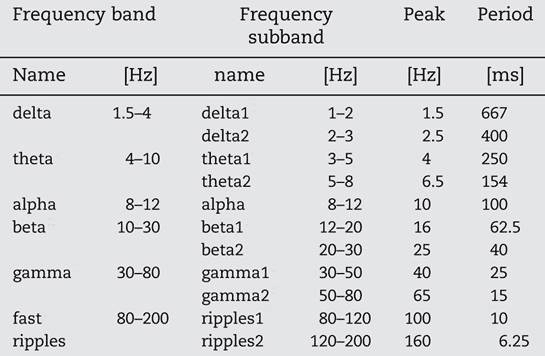
The classical frequency bands of the EEG can indeed be described as a geometric series with a ratio between neighbouring frequencies approximating F = 1.618. Not only does the ratio between neighbouring peak frequencies approximate the golden ratio, the successive frequencies are the sum of two previous, approximating the Fibonacci sequence (see [11] for the relationship between F and the Fibonacci sequence). Synchronization of the excitatory phases of the two oscillations is impossible. Thus, the golden ratio gives a totally uncoupled (yet coherent) processing state, which most likely reflects the resting brain. However, the excitatory phases of the two oscillations occasionally come close enough to coincide. These coincidences are more frequent the higher the frequencies of f1 and f2. Thus, intuitively, at least, one can see that the golden ratio provides the highest physiologically possible desynchronized state, and at the same time, the potential for spontaneous diverse coupling and uncoupling between rhythms and a rapid transition from resting state to activity. This is borne out by findings from other laboratories.
Dietmar Plenz at the US National Institute of Mental Health has identified ‘neuronal avalanches’ - cascades of neuronal activities that follow precise 1/f power laws - in the excitatory neurons of the superficial layers in isolated neocortex preparations in vitro as well as in awake animals and humans in vivo [12]. The neocortex of mammals is a sheet of 6 layers folded inside the skull. Inputs to the cortex arrive at layer IV, whereas outputs to brain structures outside the cortex are provide by neurons in deep layers V and VI. The superficial layers II and III are where cortical neurons talk to one another only, with layer I mainly composed of fibre bundles supporting intra-cortical communication. A combination of experiments, theory and modelling showed that the neuronal avalanche of the default state with the 1/f signature of self-organized criticality gives the optimum response to inputs as well as maximum information capacity.
Most interestingly, the avalanche dynamics give rise to coherence potentials, subsets of avalanches in which the precise waveform of the local field potential is replicated with high fidelity in distant network sites. The process is independent of spatial distance and includes near instantaneous neuronal activities as well as sequential activities over many time scales. Most coherence potentials are spatially disjunct, i.e., they do not obey nearest neighbour relationships. LFPs of successive coherence potentials are not similar, but they are practically identical within a coherence potential among all the participating sites, there being no growth or dissipation during propagation. This intriguingly suggests that the waveform of a coherence potential is a high-dimensional coding space in information processing of the brain. For decades, phase-locked neuronal activity has been reliably recorded using the LFPs or EEG and was found to correlate with the presentation of stimulus in animals and visual perception in humans.
Another team of researchers led by Miles Whittington at Newcastle University in the UK have begun to reveal the intricacies in the golden music of the brain by recording from multiple layers of the neocortex simultaneously. They found multiple local neuronal circuits supporting different discrete frequencies in the neocortex network, and the relationships between different frequencies appear designed to minimize interference and to allow diverse coupling of activities via stable phase interactions and the control of the amplitude of one frequency in relation to the phase of another [13]. There is even a transformation that combines the oscillations of tw0 neighbouring frequencies sequentially to generate a third frequency whose period is the concatenated sum of the original two. With such an interaction, the intrinsic periodicity in each component local circuit is preserved: alternate, single periods of each original rhythm form one period of a new frequency, suggesting a robust mechanism for combining information processed on multiple concurrent spatiotemporal scales to generate what must be the most amazing golden quantum jazz.
The 1/f pattern of EEG is really a time-averaged smoothed collection of multiple, discrete frequencies, and does not represent all the frequencies and combination of frequencies present in the brain. (It is like a recording of a Mozart symphony that averages out all the sounds made in discrete periods of time, so the music is completely buried.) Detailed observations made by the team have shown that at least three discrete frequencies d (1-3 Hz), q (6-9 Hz), and g (30-50 Hz) are often expressed simultaneously, and can be associated with further much slower rhythms both in vivo and in vitro.
Discrete frequencies ranging from low d to high g can be produced from a single area of the isolated neocortex in vitro, with peak frequencies distributed according to the golden ratio. All attempts to generate single frequencies have failed, and the phenomenon has been referred to as spectral processing.
To keep simultaneously occurring frequencies apart and minimize interferences, the solution is to have ratios of frequencies that are irrational numbers. Coexistent g1 and b2 rhythms in the cortex, for example, are generated in two different layers and survive physical separation of the layers. The ratio of peak frequencies is approximately F, resulting in a periodic pattern of change in low-level synchrony between the layers with a period equal to the sum of the two periods of oscillation present. This phenomenon can occur to some extent with any pair of co-expressed frequencies. But using F as a common ratio between adjacent frequencies in the EEG spectrum enables the neocortex to pack the available frequency space (thereby maximising the information processing capacity, or the capacity to produce the most music). If the cortex uses different frequency bands to process different aspects of incoming information, then it must also have the ability to combine information held in these bands to reconstruct the input; hence the importance of keeping them separate, as the golden ratio does.
Phase synchrony does happen, and has been seen in human recordings made with MEG (magnetoencephalography using an array of very sensitive superquantum interference device (SQUID) magnetometers) when frequency ratios are integer values. Stable phase relationships between frequencies with ratios of 2, 3, and 4 are seen during mental arithmetic tasks in localized regions of the neocortex; and the phenomenon has also been proposed to be involved in memory matching and attention.
The most readily observable form of cross-frequency interaction is that of ‘nesting’. Here the amplitude (power) of a discrete frequency band is modified according to the phase of a lower frequency coexistent rhythm. This is seen when g rhythms coexist with q frequencies in the hippocampus. Hierarchies of nested rhythms are also seen. Nesting of d, q and g rhythms exists both in the hippocampus and the neocortex. This arrangement ensures that successively high frequencies are maximally expressed in a manner dependent on the lower frequencies in the hierarchy and does not per se imply precise phase relationships, though stable phase relationships may be maintained.
It is also possible for a local circuit generating a single frequency rhythm to switch frequencies. Such changes are facilitated by a range of mechanisms including changes in neuronal intrinsic conductances and non-reciprocal interactions with other regions oscillating at a similar frequency. After stimulation, g frequencies can transform to b frequency (approximately halved) due to inhibitory postsynaptic potentials on the principal cells generating the action potentials.
An additional type of interaction, concatenation, involves a g frequency generated by a superficial layer interacting with a b2 frequency in a deep layer combining into a new frequency, b1, but the intrinsic original frequencies are preserved in that alternate, single periods of each original rhythm form one period of the new frequency. Concatenation is possible for any given pair of rhythms.
Can interactions between multiple spatiotemporal scales of activity tell us anything about how the cortex processes sensory information?
In the temporal domain, the ability of a system to sort rapidly changing features of an input from more slowly changing features provides an efficient means of recognizing objects. A hierarchical arrangement of feature detection over a range of temporal scales can reproduce many properties of individual neurons in the visual cortex. Thus, from a computational perspective, it is an advantage for the cortex to process different temporal scales of information separately, using different frequencies. It has been shown that rhythms with larger temporal scales (slower frequencies) facilitate interactions over greater distances in cortical networks, i.e., they may synchronize over larger areas of the visual map in the retina of the eyes. Thus, different frequencies may have a role for processing sensory information on different spatial scales. In a visual task designed to test perceptual shifting from features of an object with low spatial frequency to those with high spatial frequency, a direct correlation was seen between spatial scale of the sensory object and the temporal scale (frequency) of associated cortical rhythms. Thus cross-frequency phase synchronization is a possible means of combining information from different frequency channels to fully represent a sensory object.
Article first published 17/03/14
Comments are now closed for this article