Other articles in this series

1) The Story of Phi
2) Watching the Daisies Grow
3) Golden Music of the Brain
4) Golden Cycles & Organic Spacetime
5) Golden Geometry of E-Infinity Fractal Spacetime
6) E-Infinity Spacetime, Quantum Paradoxes and Quantum Gravity
7) Water Structured in the Golden Ratio

---

Science of the Organism

Golden Geometry of E-Infinity Fractal Spacetime

Story of Phi Part 5

The golden ratio is at the core of our fractal universe of infinite dimensions that looks and feels 4-dimensional. Dr. Mae-Wan Ho

Real processes do not happen at points in a spacetime continuum

Alfred North Whitehead (1861-1947) lived through what must have been a most exciting period in Western science. The very fabric of reality – the flat, smooth, and static absolute spacetime of the Newtonian universe – is being thoroughly ruffled, if not torn asunder, by Albert Einstein’s theories of special and general relativity at large scales and by quantum mechanics at the smallest.  Out goes the proverbial objective scientific observer outside nature, to be supplanted by the knower irreducibly quantum-entangled with the known, possibly with all entities in the entire universe.

These surprising and exhilarating lessons from nature became the basis of Whitehead’s perennial, universal philosophy (a cosmogony) [1], initiating a new age of the organism that has inspired generations of scientists, including me. Most enlightening though least understood was his argument on why the mechanical laws of classical physics and differential calculus fail to describe real processes. Apart from the all-important knowing experiencing organism left out of account, real processes have characteristic times (durations) and spaces (volumes). Nothing, absolutely nothing happens at a point in an instant. In other words, spacetime is not a smooth continuum; it is discrete and discontinuous, as quantum physics already discovered at the smallest scale. Indeed spacetime can more easily be conceived as being created by action, by processes that naturally occur in quantum jumps.

Unfortunately, mathematics - a major tool of thought for western science, especially physical science - had lagged somewhat behind physics. Both relativity theory and quantum theory inherited the predominant mathematics of classical mechanics.

British theoretical physicist Roger Penrose’s monumental tome, The Road to Reality, A Complete Guide to the Laws of The Universe [2] is indeed a “tour de force”, as advertised. It charts the heroic efforts of mathematical physicists to make sense of post Newtonian physics; their ingenuities and successes, as well as failures. More than a century later today, the dream of uniting the two great theories of quantum physics and general relativity has remained stubbornly beyond our grasp. And one main reason is that the two theories are divided by a common ground: a differentiable spacetime manifold.

Differentiable spacetime and differential calculus assume objects have instant point-like ‘simple locations’ in space and time. It is fundamentally at odds with physical reality, and may well be creating more problems than it can solve.  But there is still a tendency to put mathematics (and mathematical physics) on a pedestal as though it has an ‘objective’ independent existence to which physical reality must conform. This neo-Platonist view championed by Penrose [2] is surely a case of misplaced concreteness. It has been more than 80 years since Austrian mathematician and logician Kurt Gödel (1908-1978) proved his incompleteness theorems [3], which essentially state that a set of axioms both complete and consistent is nevertheless unable to guarantee a complete and consistent theory, let alone one that applies to physical reality.

Nevertheless, mathematics is a wonderful, exquisite tool for thought, and I have come to appreciate it more and more in my continuing quest for the meaning of life and the universe (see [4] The Rainbow and the Worm, The Physics of Organisms, I-SIS publication). The mathematics of non-differentiable and discontinuous spaces, which has the potential to describe physical reality more authentically, is among the most significant discoveries/ inventions beginning in the latter half of the 19^th century though it did not really blossom until well into the 20^th century.

I shall describe an intuitive and ingenious theory of spacetime that makes full use of the newer mathematics. Before proceeding, please read Box 1 for a quick guide to mathematical terms that you will be bumping into a lot in the rest of this article; and return to it as often as is necessary.

E infinity fractal spacetime looks and feels 4-dimensional

The idea that spacetime is fractal originated with Canadian mathematician Garnet Ord [4] who coined the term ‘fractal spacetime’, using a model in which particles are confined to move on fractal trajectories.  Independently, French astrophysicist Laurent Nottale proposed a scale-relativity theory of fractal spacetime [5]. As Ord reminds us [4], American quantum physicist Richard Feynman (1918-1988) had already pointed out [6] that the paths of quantum mechanical particles look more like non-differentiable curves than straight lines when examined on a fine scale.

It is Egyptian-born Mohamed El Naschie, however, who has taken us furthest towards a coherent theory of physical reality that is also closest to our intuitive notion of organic spacetime. For precisely the same reasons, perhaps, El Naschie has attracted admiration and antagonism in equal measure.

As an aside, the journal Nature initiated a smear campaign against El Naschie in 2008 with an article written by its German correspondent [7] that was filled with insinuations and innuendoes, if not outright lies.  It accuses El Naschie of “self-publishing” papers of “poor quality” without proper peer review in a theoretical physics journal of which he has been editor-in-chief. In fact, El Naschie has had hundreds of papers published in other journals; and his prolific output continued throughout the subsequent four-year period during which he brought a libel case single-handedly against Nature. El Naschie turned down all attempts by Nature to settle out of court, until the court ruled against him in 2012. By this time, Nature had spent £5 million in legal fees to defend itself. Given Nature’s shameful record in libeling myself and other scientists over the hazards of genetic modification, I became all the more determined to find out about El Naschie’s work; and have been suitably rewarded as a result.

El Naschie trained and practiced as an engineer while indulging in his hobby of cosmology, and produced a startling new theory of spacetime, which soon took over his life entirely. E-infinity, as he calls it, is a fractal spacetime with infinite dimensions. Yet its Hausdorff (fractal dimension) is 4.236067977... In other words, at ordinary resolution, it looks and feels 4 dimensional (three of space and one of time), with the rest of the dimensions ‘compacted’ in the remaining 0.236067977… “fuzzy tail”[8].

Think of a four dimensional hypercube with further four dimensional hypercubes nested inside like Russian dolls [9]. In fact, the exact Hausdorff dimension is 4 + f³, where f = (√5-1)/2, the golden ratio.  Particularly suggestive is that the dimension 4 + f³ show the following self-similar continued fraction (see Figure 1) which sums to precisely 4 + f³ at infinity:

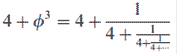
The 4-dimensional hypercube is the Euclidean representation of the E-infinity universe. It is a challenge to represent E-infinity it in its proper non-Euclidean form.

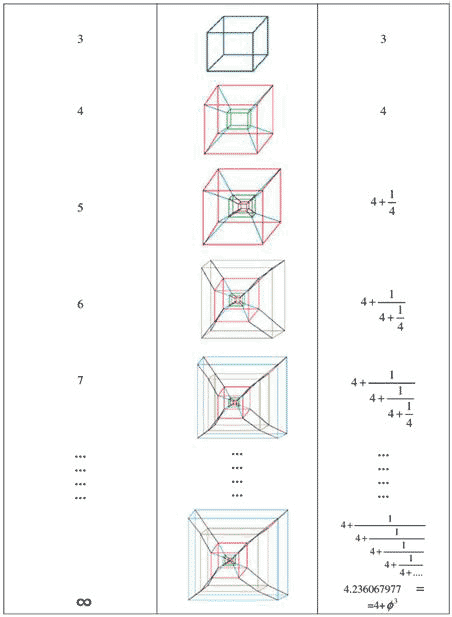
Figure 1   E infinity fractal spacetime represented as nested four dimensional hypercubes

The E-infinity universe is mathematically a random Cantor set (the simplest fractal) extended to infinite dimensions, and the remarkable result is that the limit of this infinite extension is no larger than 4 + f³.

Figure 2 depicts some of the steps involved in deriving E infinity universe. We start from the 1-dimensional Cantor set, the unit line, which is divided into three equal parts; take out the middle, and carry on the same operation on the two parts remaining, up to an infinite number of steps. At the end, there should be nothing left but isolated points (Cantor dust). Its Menger-Urysohn dimension is 0, but amazingly, its Hausdorff (fractal) dimension is ln2/ln3, for the usual triadic Cantor set; but is f = (√5-1)/2 = 0. 61803398.. for the random Cantor set, in which the section removed is not necessarily the middle one, but c0uld be any of the three parts at random. This important result, proven by American mathematicians Daniel Mauldin and S C Williams in 1986 [10], is what makes it possible to derive the E-infinity universe with all its remarkable properties, as we shall see. Another mathematical property of the Cantor set is that its cardinality (number of points or elements) is exactly the same as the original continuous line. Thus, the Cantor set is a perfect compromise between the discrete and the continuum; it is a discrete structure that has the same number of elements as the continuum.

From the 1-dimensional Cantor set, we can construct the higher dimensional spaces (see Fig.2). The 2-dimensional version is the Sierpinski gasket, with random Hausdorff dimension of 1/f = 1.61803398..; the 3-dimensional version is the Menger sponge, with random Hausdorff dimension 2 + f = 2. 61803398.. The Sierpinski gasket and Menger sponge are both well-known geometric shapes. Not so the 4-dimensional version, with random Hausdorff dimension 4 + f ³ = 4.23606797…, where only an artist’s representation is given. The 4-dimensional version is the same as the E infinity universe constructed from an infinite number of random Cantor sets (as will be made clear later). Note that the diagram is space-filling: it consists of spheres of different sizes representing space-times at different scales so that the entire volume is completely packed. This space-filling is analogous to, if not the same property as quasi-periodic Penrose tiling in 2 dimensions of Euclidean (flat) space where the golden ratio is key (see [11] The Story of Phi Part 1, SiS 62), as it is in E infinity universe. And incidentally, branching processes based on the golden ratio are also space-filling [12], as are spiral leave arrangement patterns with the golden angle between successive leaf primordial (see [13] Watching the Daisies Grow, SiS 62).

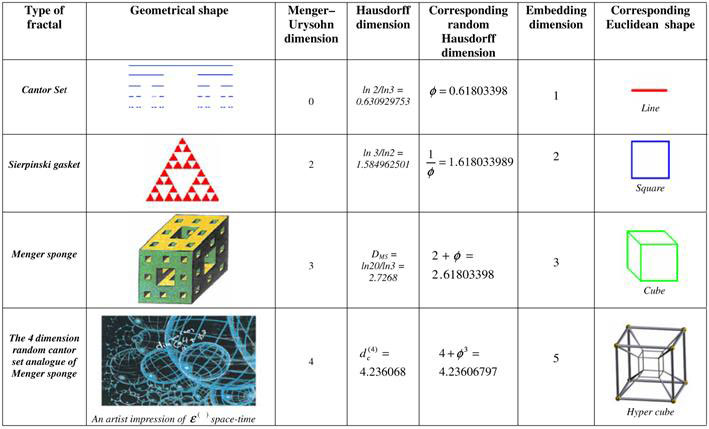
Figure 2   Fractals and dimensions in the derivation of E infinity spacetime

El Naschie has presented multiple formal derivations of E infinity spacetime, I shall give the one relying on the mathematical properties of Borel sets to which Cantor sets belong. It is so simple that even a non-mathematician can understand it.

The expectation value of the Hausdorff dimension of the Cantor set extended to infinity is simply a sum over n , for n = 0 to n = ∞, of n multiplied by the Hausdorff dimension of the random Cantor set raised to the power n. This is more concisely encapsulated in the following equation:

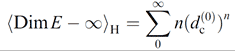                                                             (1)

where the left hand side is the expectation value of the Hausdorff dimension of the Cantor set extended to infinity; the superscript in d_c⁽⁰⁾ refers to the Menger-Urysohn dimension of the random Cantor set, which is 0, while the corresponding Hausdorff dimension d_c⁽⁰⁾ is f. The summing up of the infinite number of terms gives the answer 4 + f³ exactly.

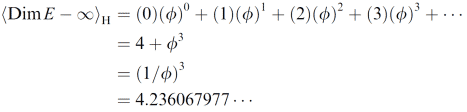                  (2)

Now, the intersection rule of sets, also known as the bijection formula, which relates the Menger-Urysohn dimension to the Hausdorff dimension, shows that we can lift d_c⁽⁰⁾  to any Menger-Urysohn dimension n to arrive at the correct Hausdorff dimension d_c⁽ⁿ⁾ as follows:

d_c⁽ⁿ⁾ = (1/ d_c⁽⁰⁾) ^n-1                                                                                                      (3)

Taking d_c⁽⁰⁾ =  f, and lifting to n = 4 dimensions gives

d_c⁽⁴⁾ = (1/ d_c⁽⁰⁾) ^4-1 = 4 + f³ = 1/f³ = 4.236067977…

                                                  = ⟨Dim E ˗ ∞⟩_H                                                                        (4)

In other words, the expectation value of the Hausdorff dimension of E infinity universe is the same as that of a universe with a Menger-Urysohn dimension of 4. That is why E infinity is a hierarchical universe that looks and feels 4 dimensional (it is strictly embedded in 5 dimensions, see Fig. 2).

E-infinity, Penrose tiling, and Fibonacci sequence

The E-infinity universe is intimately connected with Penrose tiling and the Fibonacci sequence (see [11]) through E-infinity algebra [14, 15]. In his important book Noncommutative Geometry [16], French mathematician Alain Connes identified Penrose’s fractal tiling as a mathematical quotient space (a space of points ‘glued together’ by an equivalence relationship), with the following dimensional function:

D(a, b) = a + bf                                                                                               (5)

Where a, b are integers (whole numbers) and f = (√5-1)/2. Writing D_n (a_n, b_n) with the Fibonacci sequence, it is easy to see that starting with D₀ = D (0, 1) and D₁ = D (1, 0), the following dimensional hierarchy is obtained:

D₀ = D (0, 1) = 0 + f = f

D₁ = D (1, 0) = 1 + (0)f = 1

D₂ = D (0+1, 1+0) = 1 + f = 1/f

D₃ = D (1+1, o+1) = 2 + f = (1/f)²

D₄ = D (1+2, 1+1) = 3 + 2f = (1/f)³

D₅ = D (2+3, 1+2) = 5 + 3f = (1/f)⁴

D_n(a_n, b_n) = D {(a_n-1, a_n-2) + (b_n-1 + b_n-2)}f = (1/f)^n-1                                        (6)

Not that for D₄ (dimension 4), the Fibonacci number is (1/f)³ = 4 + f³, exactly the Hausdorff dimension of a Menger-Urysohn 4-dimensional space.

By induction,

D_n = (1/f)^n-1                                                                                                                 (7)

which is identical to the bijection formula from E-infinity algebra (see Eq (3) above):

d_c⁽ⁿ⁾ = (1/f) ^n-1                                                                                                             (8)

The summing of random Cantor sets to infinity is very suggestive of spacetime being created or constructed by actions over all scales, from submicroscopic to macroscopic and beyond, which is close to what I have envisaged [4], following Whitehead [2] and German theoretical physicist Wolfram Schommers [17].

E infinity spacetime can also resolve major paradoxes within quantum theory and produce new results as we shall see in the next article [18] (E Infinity Spacetime, Quantum Paradoxes and Quantum Gravity, SiS 62).

Article first published 31/03/14

---

References

1. Whitehead AN. Science and the Modern World, Lowell Lectures 1925, Collins Fontana Books, Glasgow, 1975.
2. Penrose R. The Road to Reality, A Complete Guide to the Laws of the Universe, Vintage Books, London, 2005. 1 099 pp.
3. Gödel’s incompleteness theorems. Wikipedia, 26 February 2014, http://en.wikipedia.org/wiki/G%C3%B6del%27s_incompleteness_theorems#Construction_of_a_statement_about_.22provability.22
4. Ho MW. The Rainbow and the Worm, the Physics of Organisms, World Scientific, 1993, 2^nd edition, 1996, 3^rd enlarged edition, 2008, Singapore and London. https://www.i-sis.org.uk/rnbwwrm.php
5. Ord GN. Fractal space-time: a geometric analogue of relativistic quantum mechanics. J Phy A: Math Gen 1983, 16, 1869-84.
6. Nottale L. Fractal Space-Time and Microphysics: Towards a Theory of Scale Relativity, World Scientific, 1993.
7. Feyman RP and Hibbs AR. Quantum Mechanics and Path Integrals, McGraw-Hill, New York, 1965.
8. “Self-publishing editor set to retire”, Quirin Schiermeier, Nature 2008 456, 432.
9. El Naschie MS. A review of E infinity theory and the mass spectrum of high energy particle physics. Chaos Solitons & Fractals 2004, 19, 209-36.
10. Mauldin RD and Williams SC. Random recursive constructions: asymptotic geometric and topological properties. Trans AM Math Soc 1986, 295, 325-46.
11. Ho MW. The story of phi part 1. Science in Society 62 2014.
12. “There is something about phi, Chapter 9 - Fractals and the golden ratio” Javier Romanach, YouTube, accessed 1 March 2014, http://www.youtube.com/watch?v=BURjKRfOA9g
13. Ho MW. Watching the daisies grow. Science in Society 62 2014.
14. El Naschie MS. The theory of Cantorian spacetime and high energy particle physics (an informal review). Chaos, solitons and Fractals 2009, 41, 2635-46.
15. Marek-Crnjac L. The Hausdorff Dimension of the Penrose universe. Phys Res Interna 2011, 874302, 4 pages
16. Connes A. Noncommutative Geometry, Paris, 1994, http://www.alainconnes.org/docs/book94bigpdf.pdf
17. Schommers W. Space-time and quantum phenomena. In Quantum Theory and Pictures of Reality (W. Schommers ed.), pp. 217-77, Springer-Verlag, Berlin, 1989.
18. Ho MW. E infinity spacetime, quantum paradoxes and quantum gravity. Science in Society 62 2014.