Other articles in this series

1) The Story of Phi
2) Watching the Daisies Grow
3) Golden Music of the Brain
4) Golden Cycles & Organic Spacetime
5) Golden Geometry of E-Infinity Fractal Spacetime
6) E-Infinity Spacetime, Quantum Paradoxes and Quantum Gravity
7) Water Structured in the Golden Ratio

---

Science of the Organism

E-Infinity Spacetime, Quantum Paradoxes and Quantum Gravity

Story of Phi Part 6

E-infinity fractal spacetime may resolve major quantum paradoxes and take us further towards the unification of quantum physics and general relativity. Dr. Mae-Wan Ho

E-infinity fractal spacetime is constructed from an infinite number of random Cantor sets, and is therefore infinite-dimensional. Nevertheless it has a Hausdorff dimension of 4 + f³ = 4.236067977..., the same as that of a space with 4 Menger-Urysohn dimensions, which is why E-infinity looks and feels like a 4-dimensional universe that we actually live in. (You may want to reread [1] Golden Geometry of E-Infinity Fractal Spacetime, SiS 62 before proceeding.) More importantly, at least as far as physics is concerned, it may resolve some major quantum paradoxes and take us towards quantum gravity and the dream of uniting quantum physics with general (and special relativity).

El Naschie has used E-infinity algebra to solve quantum conundrums, presenting multiple derivations if not proofs. Let’s look at some of them.

Wave particle duality, the zero and the empty set

The wave-particle duality of light and matter is among the greatest paradoxes in quantum mechanics, as clearly exhibited in the two-slit experiment (Figure 1). A source of light is placed in front of a screen with two narrow slits that allow light to pass through to strike a photographic plate behind the screen.

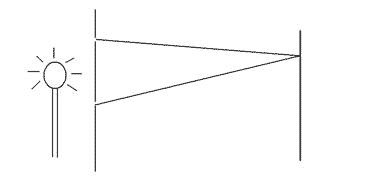
Figure 1   The two-slit experiment

When only one slit is open, the light passes through the single slit and hits the photographic plate forming an image of the slit, which when examined closely, consists of microscopic grains of silver deposited as the individual photon particles impinge on the plate. When both slits are open, light passes through both slits and form an interference pattern on the photographic plate, behaving like typical waves up until the moment the wave strikes the plate (see Figure 2).

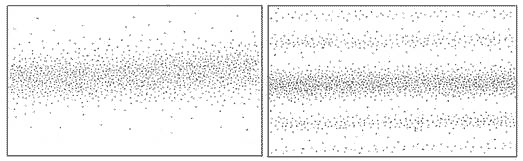
Figure 2   The pattern on the photographic plate with one slit open (left) and two slits open (left)

One can reduce the light level to such an extent that only single photons are emitted one at a time; and if both slits are open, the single photon would still pass through both slits at once and create an interference pattern on the photographic plate, which is detected after a suitably long period of time when sufficient single photons have gone through. If one puts a detector behind a slit to try to find out which slit the single photon has gone through, then the pattern reverts to that of the single slit. It is as though the observer must remain ignorant as to which slit the photon passes through for the quantum wave to survive intact. Any observation or attempt to gain information will ‘collapse’ the wave function, so only the particle remains.

The way this paradox can be resolved is through the E-infinity algebra of the zero and the empty set [2].

Remember that a one-dimensional Cantor set has both a Menger-Urysohn dimension and a Hausdorff dimension. The random Cantor set has a Menger-Urysohn dimension of 0 while its Hausdorff dimension is f. It is called the zero set, and El Naschie proposes to identify this zero set with the particle:

                              dim (particle set) =  P(d_MU, d_H) = P (o, f)                                                      (1)

where d_MU is the Menger-Urysohn dimension and d_H is the corresponding Hausdorff  dimension.

The quantum wave on the other hand, is identified with the empty set, as it is devoid of matter and momentum as it is spread out ultimately over the entire universe:

                              dim (wave set) =  W(d_MU, d_H) = W (-1, f²)                                                     (2)

How does one get to this empty set? You get there by a process of induction as follows.

What is the dimension of a 3D cube boundary? It is clearly an area, i.e., a surface of 2D. That means

                              3D(cube) – 1 = 2D (surface)

Next, what is the dimension of the boundary of a 2D surface? It is obviously a one-dimensional line.

                              2D(surface) -1 = 1D (line)

Finally, what is the dimension of the boundary of a line? This is evidently a zero dimensional point

                              1D(line) – 1 = 0D (point)

By induction, one could write a general expression for the above in the form of:

                              D(boundary) = n – 1                                                                 (3)

where n is the dimension of the geometrical object for which we would like to know the dimension of its boundary. By induction, using this formula, we can derive the boundary of a point:

                              D(boundary) = D(point) – 1 = 0 – 1 = -1

This is the dimension of the classical empty set as deduced for the first time by Soviet Russian mathematician Pavel Urysohn (1898-1924) and studied by Austrian American mathematician Karl Menger (1902-1985), which is the origin of the Menger-Urysohn topological dimension. Its Hausdorff dimension is obtained by the bijection formula you have already come across earlier (see [1]) as f².

                              d_c⁽ⁿ⁾ = (1/ d_c⁽⁰⁾) ^n-1                                                                        (4)        

                              d_c^(-1) = (1/ d_c⁽⁰⁾) ^n-1

                                       = (1/f)^-2 = f²

The quantum wave is thus identified as the boundary of the particle, which is completely empty, with a Menger-Urysohn dimension -1, but nevertheless possesses a Hasudorff fractal dimension f². The empty set is de facto two identical things at the very same time, the surface or the topological neighbourhood of the zero set as well as being the guiding quantum wave. The zero set is a Cantorian fractal point as well as the quantum particle guided by the ‘ghost’ wave. This may be understood in a very elementary manner, according to El Naschie, by recalling that the wave is the surface of the particle and it is evident that the smaller, say a sphere, the larger is the ratio between its surface area  and its volume. When the volume tends to zero, the ratio will tend to infinity.

Now, on taking measurement on this particle-wave packet, we inevitably enter into the wave and consequently into the domain of the empty set. So the empty set becomes non-empty and “practically reduced or jumps to at best, a zero set.”

Wave particle duality and dark energy

Continuing in the same vein, El Naschie proposes that Einstein’s famous formula E = mc² consists of two parts. The first part is the positive energy of the quantum particle modeled by the topology of the zero set. The second is the absolute value of the negative energy of the quantum Schrödinger wave modeled by the topology of the empty set [3] (see above). The latter is the missing dark energy (actually dark energy and dark matter) of the universe accounting for 95.45 % of the total energy-matter in agreement with the findings from the Wilkinson Microwave Anisotropy Probe and the supernova cosmic measurement awarded the 2011 Nobel Prize in Physics. The dark energy of the quantum wave cannot be detected in the normal way because measurement collapses the quantum wave. Several recent attempts to detect dark matter with sophisticated detectors have failed [4] No Dark Matter Detected Yet (SiS 62), which is potentially devastating for the standard model of cosmology that depends on postulates of dark matter and dark energy.

The Menger-Urysohn dimension and Hausdorff dimension of a random Cantor set are [o, f] [3]. The dimensions of the complement (gaps) are [-1, and  1 – f = f²], as established above.

Raising both the f (points) and f² (gaps) set to the Kaluza-Klein 5 dimensional spacetime gives f⁵ (volume) and 5f² (boundary) and respectively equal to 4.5 % and 95.5 % of Einstein’s energy, the latter corresponding to dark energy/matter.

(Different estimates of dark matter and dark energy vary somewhat. According to the latest figure, dark energy plus dark matter constitute 95.1 % of the total content of the universe [5].)

The Kaluza-Klein 5 dimensional spacetime attempted to unify gravity with electromagnetism [6]. It originated with German mathematician physicist Theodor Kaluza (1885-1954) who extended general relativity to a five-dimensional spacetime to include the electromagnetic field. Swedish theoretical physicist Oskar Klein (1894-1977) later propose that the extra fourth spatial dimension is curled up, or compactified,  in a circle of very small radius, so that a particle moving a short distance along that axis would return to where it began. This compactification of dimensions is now widely employed in string theories that attempt to give a realist explanation of why the universe looks and feels 4 dimensional (see Box). There may well be a more intimate relationship between the Kaluza-Klein spacetime and E-infinity spacetime, which El Naschie has not pointed to, though it is implicit in his work. Recall that the embedding dimension for E-infinity space-time of Hausdorff dimension 4 + f³ = 4. 236067977 is also 5, and the fuzzy tail of 0. 236067977 is the compactified (∞ - 4) dimensions. If we equate 0.236067977 = f³ with the sum of ordinary matter and energy that we can detect, and ask what percentage it is of the transfinite dimension of the Kaluza-Klein 5 dimensional spacetime, 5+ f³, we get 4.5 %. In other words,

                              f³/(5+ f³) = .04721359…. ≈ 4.5 %

which gives 95.5 % dark matter/energy.

Thus, the compactified spacetime dimensions is likened to the super-particle of the universe, while the rest is the empty-set ‘halo’ and quantum wave that collapses as soon as it is measured. If that is the case, neither dark matter nor dark energy would be detected.

Quantum entanglement and E-infinity

Quantum entanglement is another quantum paradox where the quantum states of different particles are inseparable even when they are far apart, so that measuring the state of one instantly determines the state of the other. This has been demonstrated, not just for particle/antiparticle pairs that are created together and so expected to be correlated, but also for particles independently generated, that when made to interact, will become entangled. This is an extremely active field of research that has implications for quantum communication and computation, and even teleportation [9].

In 1992, theoretical physicist Lucien Hardy, then at Oxford University in the UK, now at Perimeter Institute for Theoretical Physics Waterloo, Canada, proposed a thought experiment that predicted a probability of quantum entanglement at ~ 9 % [10]. This was re- derived and interpreted by American solid state physicist David Mermin at Cornell University, New Haven, Connecticut who first noticed the connection to the golden ratio [11], and also American theoretical physicist Daniel Styer at Oberlin College, Ohio [12].

It turns out that this probability of quantum entanglement can be derived using pure logic and E-infinity theory, as El Naschie showed [13].

Consider two particles; the probability to be at point 1 is d₁, while the probability of being at point 2 is d₂. Consequently, the probability of not being at 1 is 1 - d₁, and not being at two is 1 - d₂. The total probability of being all of the above at the same time - a distinctive quantum property of entanglement - is:

                              P₁ = d₁(1 - d₁)d₂(1 - d₂)                                                                              (5)

The simplest local realism (classical, non-quantum property) is the negation of being at 1 and 2 at the same time. This non-entangled state is,

                              P₂ = 1 - d₁d₂                                                                                                                                   (6)

A relative probability is defined as

                              P = P₁/P₂

                              P = [d₁(1 - d₁)d₂(1 - d₂)]/(1 – d₁d₂)                                                         (7)

Next, find an extremum (maximum or minimum) for P where P is a maximum, i.e., when the change of P with d₁ and d₂ are both zero:

                              ∂P/d₁ = ∂P/d₂ = 0            

This results in a cubic algebraic equation with three solutions for d₁ = d₂ = 1, -1/f and f.                The third solution f is a confirmation of E-infinity theory where d_c⁽⁰⁾ = f is both the Hausdorff dimension of a random triadic Cantor set as well as  the topological probability of finding a Cantorian point in this set. To obtain Hardy’s result explicitly, we insert d₁=d₂= f into Eq (7) for P and find

                              P = f⁵ ≈ .0909829…

This probability can also be derived directly from E-infinity theory as follows.  The probability of finding a point in the E infinity space is f³, the inverse of 4+ f³, the Hausdorff dimension of E-infinity spacetime.

The general formula for the dimension is

                              ⟨n⟩ = (1 + d_c⁽⁰⁾)/(1 - d_c⁽⁰⁾)                                                                         (8)

 Consequently the probability is

                              1/⟨n⟩ = (1 - d_c⁽⁰⁾)/(1 + d_c⁽⁰⁾)        

The probability of two entangled points in this space is (d_c⁽⁰⁾)², i.e., the Hausdorff dimension of the points multiplied together.

Consequently, the total probability of entanglement is the product of 1/⟨n⟩ and (d_c⁽⁰⁾)².

                              P = (d_c⁽⁰⁾)²[(1 - d_c⁽⁰⁾)/(1 + d_c⁽⁰⁾)]

On maximizing P or from E-infinity theory, d_c⁽⁰⁾ = f and 1/f. Inserting d_c⁽⁰⁾ = f, we get Hardy’s result again

                              P = f⁵

To obtain the result P = 0 of the classical (no entanglement) expectation, we set d_c⁽⁰⁾ = d_c⁽¹⁾ = 1.

From the preceding derivations, it seems clear that Hardy’s result is geometrically and topologically rooted in the Cantorian nature of microquantum spacetime.  This is in line with Einstein’s general relativity representation of mass and energy as geometry (curvature) of spacetime.

Quantum entanglement and dark energy

Perhaps the most audacious feat with E-infinity algebra is a new quantum gravity formula predicting the measured cosmic energy content of the universe, by fusing the probability of quantum entanglement with Einstein’s E = mc² formula, thereby unifying relativity and quantum mechanics.

Essentially, Einstein’s celebrated equation is multiplied by a scaling parameter g = f⁵/2, where f⁵ is half the probability of quantum entanglement [14].

Einstein’s equation is replaced by an effective quantum gravity formula:

                              E_QR = g_QR mc² = [1/2(1 – b)/(1 + b)] mc²                                (8)

which recovers Newton’s kinetic energy E = ½ mv², when b is set to 0 or 3; while setting b = 4 + f³ or b = f results in Einstein’s non quantum but relativistic formula E = mc².

In particle physics, it is proposed that at the Planck energy scale of around 1.22 x10¹⁹ GeV, which corresponds by mass energy equivalence E = mc² to the Planck mass 2.17659 x 10^-8 kg, the quantum effects of gravity becomes strong and expected to be comparable to other forces; and it is theorized that all the fundamental forces are unified at that scale, though the exact mechanism of this unification remains unknown [15].

At the other extreme of huge distances, quantum corrections accumulate and relativity cannot ignore quantum effects. Hence Einstein’s E = mc² is a candidate for major modification when the quantum mechanical effect of entanglement is taken into account. The new equation is E_QR = (f⁵/2)mc² representing a synthesis of Newton, Einstein and quantum mechanics.

Quantum relativity theory is seen as the intersection of three fundamental theories of physics, hence predicts only 4.5 % of the mass-energy in Einstein’s E = mc² equation, in accordance with cosmological measurement, with the rest being dark matter-energy.

There are four steps in generalizing E = mc² of special relativity to quantum relativity or effective quantum gravity formula E_QR =g_QR = (mc²)/22.1803989.. (the relevance for the denominator will be explained later).

The first step transforms space, time and mass to a probabilistic space, time and mass using quantum mechanics, leading to E_p = (P/2)mc² where P is the quantum entanglement probability. Second, a special form of E_R = gmc² is derived where g is a function of a special relativity correction for the unit interval b. Third, E_p is equated to E_R to find the exact value of b for which E becomes a maximum.

The probability of quantum entanglement of two quantum particles in Lucien Hardy’s thought experiment as derived in Eq (7) above is:

                              P = [p₁ (1 –p1)p₂(1 – p₂)]/(1 - p₁p₂)                                                                      (9)

                              For p₁ = p₂ = d, the expression simplifies to:

                              P = d² (1 –d)/(1 + d)                                                                                                 (10)

Now, introducing the probabilistic transformation:

                              Space (X) →  xp

                              Time (T) → tp

                              Mass (M) → mp                                                         

Inserting into Newton’s kinetic energy, one finds the following probabilistic energy for v → c (velocity approaching the speed of light)

                              E_p = ½ mp (xp/tp)² = ½ mp (v→ c)²                                                                                        (11)

Substituting  p in Equation (3) for the probability of entanglement in Eq (2) gives:

                              E_p = ½ d²[(1 –d)/(1 + d)] mc²                                                                                (12)       

From relativity theory three phenomenological effects are well known: time dilation, length contraction and increase in mass when velocity approaches the speed of light. This is represented by some unspecified correction factor b.

                              x → x(1 – b)

                              t → t(1 + b)                                                                                                                 (13)

                              m → m(1 + b)

Consequently, Newton’s relativistic kinetic energy becomes

                              E_R = ½ mc² (1 + b) [(1 – b)/(1 + b)]²  = ½ [(1 – b)²/(1 + b)] mc²                   (14)

The next step to arrive at an effective quantum gravity E is to require

                              E_P  =  E_R                                                                                                                        (15)

Therefore,

                              d²[(1 –d)/(1 + d)] = [(1 – b)²/(1 + b)]                                                                  (16)

This is only possible for d = b and

                              b² [(1 – b)/(1 + b)] = [(1 – b)²/(1 + b)]                                                                 (17)

which leads to the simple quadratic equation

                              b²  + b  - 1 = 0                                                                                                             (18)

and the solutions: b₁ = f = (√5-1)/2 the golden ratio, and b₂ = -1/f.

In the fourth and final step, the correct expression for the quantum gravity formula is given by setting d = b = f into Eq. (6)

                              E_QR = ½ f ²[(1 – f)/(1 + f)] mc²                               

                              = ½ f ²f ³ mc²  = (f⁵/2) mc²  =  mc²/22.18033989                                   (19)

                              = (probability of quantum entanglement)/2) mc²            

Eq (19) E_QR = mc²/22.18033989 approximates E_QR = mc²/22, and can be given different simple interpretations. First, the factor 22 can be regarded as what remains of the 26 dimensions of string spacetime of the original bosonic strong interactions theory (see Box) after subtracting Einstein’s 4 dimensions. Then, the 26-4 = 22 dimensions “dilute” the energy content of the cosmos and reduce it from 100/22 ~4.5 %, in agreement with the cosmological measurement of the three 2011 Nobel Laureates.

This interpretation of energy content is not quite the same as that in the previous sections. Intriguingly, the link to quantum entanglement not only combines quantum theory with gravity, but suggests that gravity may be a form of quantum entanglement (though El Naschie himself has not said so).

Golden ratio and transfinite corrections to integer dimensional symmetry groups of string theories

The significance of the golden ratio lies in the extension of the concept dimensions, originally applying only to integers, to non-integers. All high energy particle physics theories are currently constrained to Lie algebra groups with integer dimensions that are also a differentiable manifold. Just as the concept of dimension has been expanded from integer topological to a non-integer Hausdorff dimension, the same could be done for a Lie manifold. In fact, irrational small corrections to integer Lie group dimensions would be a blessing for the overall model. Gauge anomalies (anomalies under transformation) in the standard model arise from the clash of integer symmetries (invariant properties under transformation). With transfinite (beyond the finite, but not absolute infinite) irrational corrections, i.e., fuzzy tail added or subtracted from the original integer dimension, we get fuzzy symmetry group dimensions that fit together harmoniously and eliminate gauge anomalies. 

A simple example is the vital role of the golden ratio in Penrose tiling of the plane, without which, nothing would fit, and we end up with gaps or overlaps. Similarly, of the five Platonic solids, two of the most important, the icosahedron and dodecahedron, depend on the golden ratio. British-born Canadian geometer Harold Scott MacDonald Coxeter (1907-2003) extended those to four dimensional ‘polytopes’, which could not be constructed without the golden ratio. Now, the skeleton upon which the most important symmetry group used in superstring theory, the E8 exceptional E group, could be constructed from two 600 cells Coxeter polytopes by sliding a smaller one inside a larger one. The result is the E8 Gosset, which is once again based on the golden ratio.

For example, the dimension of the special orthogonal group SO(n) is

Dim (SO(n)) = n (n – 1)/2. For n = 4, the dimension is 6. If we take n to be the Hausdorff dimension of the E-infinity manifold, i.e., 4 + f³, the dimension is 6.854102.., i.e., 0.852102.. larger. This transfinite tail makes all the difference. Take 20 copies of the Lie group dimension for n = 4 + f³, then the total dimension will be 137.082039. This is the exact transfinite version of the inverse electromagnetic fine-structure constant, a, a fundamental dimensionless physical constant that characterizes the strength of the electromagnetic interaction, the currently accepted value is 7.29734257 x 10^-3 [18]

In a series of detailed calculations which is being the scope of this article, El Naschie shows that the inverse electromagnetic fine-structure constant and the golden ratio are embedded in the mass spectrum of the elementary high energy particles. To El Naschie [19] “the mass spectrum of high energy particles resembles a non-linear dynamical symphony where everything fits with everything else. We could start virtually anywhere and derive everything from everything else.”

Article first published 07/04/14

---

References

1. Ho MW. Golden geometry of E-infinity fractal spacetime. Science in Society 62 (to appear) 2014.
2. El Naschie MS. Quantum collapse of wave interference pattern in the two-slit experiment: a set theoretical resolution. Nonlinear Sci Lett A 2011, 2, 1-8.
3. El Naschie MS. Topological-geometrical and physical interpretation of the dark energy of the cosmos as a “halo” energy of the Schrödinger quantum wave. J Mod Phys 2013, 4, 591-6.
4. Ho MW. No dark matter detected. Science in Society 62 2014.
5. “Planck captures portrait of the young universe, revealing earliest light”, University of Cambridge, 21 March 2013. http://www.cam.ac.uk/research/news/planck-captures-portrait-of-the-young-universe-revealing-earliest-light
6. Kaluza-Klein theory, Wikipedia, 25 January 2014, http://en.wikipedia.org/wiki/Kaluza%E2%80%93Klein_theory
7. String theory. Wikipedia, 26 February 2014, http://en.wikipedia.org/wiki/String_theory
8. Supersymmetry. Wikipedia, 6 February 2014, http://en.wikipedia.org/wiki/Supersymmetry
9. Quantum entanglement. Wikipedia, 1 March 2014, http://en.wikipedia.org/wiki/Quantum_entanglement
10. Hardy L. quantum mechanics, local realistic theories, and Lorentz-invariant realistic theories. Phys Rev Letts 1992, 68, 2981-4.
11. Mermin D. Quantum mysteries refined. Am J Phys 1994, 62, 880-7.
12. Styer DF. The Strange World of quantum Mechanics, Cambridge University Press, Cambridge 2000, pp 54-55
13. El Naschie MS. Quantum entanglement as a consequence of a Cantorian micro spacetime geometry. J Quant Inform Sci 2011, 50-53.
14. El Naschie MS. Topological-geometrical and physical interpretation of the dark energy of the cosmos as a “halo” energy of the Schrödinger quantum wave. J Mod Phys 2013, 4, 591-6.
15. Planck scale. Wikipedia, 31 December 2013, http://en.wikipedia.org/wiki/Planck_scale
16. El Naschie MS. A resolution of cosmic dark energy via a quantum entanglement relativity theory. J Quant Inform Sci 2013,3, 23-26.
17. El Naschie MS. The theory of Cantorian spacetime and high energy particle physics (an informal review). Chaos, Solitons and Fractals 2009, 41, 2635-46.
18. Fine structure constant. Wikipedia, 25 February 2014. http://en.wikipedia.org/wiki/Fine-structure_constant
19. El Naschie MS. A review of E infinity theory and the mass spectrum of high energy particle physics. Chaos Solitons & Fractals 2004, 19, 209-36.