Science of the Organism
The golden ratio orchestrates all of nature’s cycles to create organic spacetime. Dr. Mae-Wan Ho

Circle map Wikimedia
Nature is replete with cycles and oscillations, from subatomic vibrations to planetary motion, solar cycles and beyond. Some say even the Universe cycles through deaths and rebirths. Not just Buddhists, but distinguished British theoretical physicist Roger Penrose at Oxford University and his co-author Armenian cosmologist Vahe Gurzadyan at Yerevan Physics Institute have drawn the same conclusion, based on data collected by NASA’s WMAP (Wilkinson Microwave Anisotropy Probe) satellite [1].
Gurzadyan analysed seven years of microwave data from WMAP as well as data from the BOOMERanG balloon experiment in Antarctica, and found concentric circles in the microwave background in which the range of the radiation’s temperature is markedly smaller than elsewhere. Penrose and Gurzadyan said these circles enable one to “see through” the Big Bang into the previous aeon; they are the signature left behind by the spherical ripples of gravitational waves generated when black holes collided.
These ripples or gravitational waves have been confirmed 4 years later by the BICEPS (The Background Imaging of Cosmic Extragalactic Polarization 2) experiment at the South Pole, and announced to the press with great fanfare, promising the world “a whole new era” in physics [2].
Cycles may well be involved in organizing the entire Universe; but it is in living systems that their pivotal role is most clearly defined [3] The Rainbow and the Worm, The Physics of Organisms (ISIS publication). Cyclic activities create a nested fractal hierarchy of organic space times that simultaneously maximizes global cohesion and local freedom, thereby enabling organisms to transfer and transform energy most rapidly and efficiently, as and when required.
In [4] (Golden Music of the Brain - Story of Phi Part 3, SiS 62), we saw that the golden ratio is prominent in the ‘resting’ rhythms of the brain, thereby ensuring the highest degree of asynchrony for diverse activities (freedom from interference), providing the maximum possibility for spontaneous diverse interactions between rhythms and rapid transition from resting to active state. This suggests that the golden ratio is involved in organizing cyclic activities for maximum local freedom and global cohesion, as in ‘quantum jazz’ [3].
In this article, we delve more deeply into cyclic activities and how the golden ratio works its magic for organic spacetime.
Cycles are intimately tied to the study of dynamical systems, beginning with celestial mechanics. Planets move around the sun in yearly cycles; and the great English physicist Isaac Newton (1642-1727) tried to describe the planetary cycles in terms of his laws of motion more than 300 years ago.
Newton wrote down differential equations for dynamical systems consisting of massive bodies interacting through gravitational forces. If there are only two bodies, these equations can be explicitly solved and one finds that the bodies revolve on ellipses around their centre of mass. If there is a third body – the ‘three-body problem’ – no exact solution exists even if, as in the solar system, two of the bodies are much lighter than the third [5]. So, why is the solar system stable? Or is it? We shall come back to this pressing question later.
Dynamical systems of planets can be treated mathematically as oscillators. A harmonic oscillator has a certain natural frequency. When subjected to an external force of the same frequency, resonance occurs and the motion of the oscillator becomes unbounded or unlimited. For a typical nonlinear oscillator, whenever the perturbing force has a frequency that is a rational multiple of the natural frequency of the oscillator, i.e., in whole number or fractions of whole numbers (such as ½, 2/3, 5/8, etc.) resonance will occur. Similarly, in the motion of planets around the sun, one planet exerts a periodic force on the motion or a second, and if the orbital periods of the two are rational multiples, this can lead to resonance and instability.
In 1954, Soviet mathematicians Andrey Kolmogorov (1903-1987) suggested a way of solving the problem. First, linearize the problem about an approximate solution and solve the linearized problem, then, inductively improve the approximate solutions by using the solution of the linearized problem as the basis of a Newton’s method argument. (A linear problem is one where a small change in one variable produces a correspondingly small change in another continuously.) These ideas were fleshed out over the next decade by Russian mathematician Vladimir Arnold (1937-2010) and German-American mathematician Jürgen Moser (1928-1999), resulting in the Kolmogorov Arnold and Moser (KAM) theorem. The KAM theorem is very important for understanding how cyclic activities interact with one another.
The three mathematicians were investigating the behaviour of integrable (solvable) Hamiltonian systems defined by momentum (mass x velocity) and position. The trajectories (paths of motion) of Hamiltonian systems in phase space - mathematical space representing all possible states - are confined to a doughnut-shaped surface, an invariant torus. Different initial conditions will trace different invariant concentric tori in phase space, separated by unstable chaotic regions, where the motion is irregular and unpredictable.
The KAM theorem states that if the system is subjected to a weak nonlinear perturbation, some of the invariant tori are deformed and survive, while others are destroyed [6]. The ones that survive are those that have “sufficiently irrational frequencies” (the non-resonance condition, so they do not interfere with one another). The golden ratio being the most irrational number is often evident in such systems of oscillators. It is also physically significant in that circles with golden mean frequencies are the last to break up in a perturbed dynamical system, so the motion continues to be quasi-periodic, i.e., recurrent but not strictly periodic or predictable.
An important consequence of the KAM theorem is that for a large set of initial conditions, the motion remains perpetually quasi-periodic, and hence stable. KAM theory has been extended to non-Hamiltonian systems and to systems with fast and slow frequencies.
The KAM theorem become increasingly difficult to satisfy for complex systems with more degrees of freedom; as the number of dimensions of the system increases, the volume occupied by the tori decreases. Those KAM tori that are not destroyed by perturbation become invariant Cantor sets, or Cantori; and the frequencies of the invariant Cantori approximate the golden ratio.
The golden ratio effectively enables multiple oscillators within a complex system to co-exist without blowing up the system. But it also leaves the oscillators within the system free to interact globally (by resonance), as observed in the coherence potentials that turn up frequently when the brain is processing information (see [4] ). To get a better picture, we look at the circle map.
Cycles are often represented by the circle map, a graph that maps the circle onto itself. The simplest form is [7, 8]:
qn+1 = qn + W – (K/2p) sin2pqn (1)
Where the variable qn+1 is computed mod 1 (meaning counting only partial circles, as full circles get back to the starting point), K is the coupling strength, W is the external driving frequency. This model describes oscillatory systems from solid state physics to heart rhythms. The circle map tracks the universal behaviour of dynamical systems associated with transition from cycles to chaos via quasi-periodicity.
The most studied circle map involves a ratio of basic frequencies w = f = (√5 – 1)/2, the ‘golden mean critical point’ at K =1 and W = Wc = 0.60666106347011 (≈ f = 0.618033989…), reported in many experiments in which universal numbers associated with the golden ratio were observed and documented.
Circle maps contain some key features.
Arnold tongues
Arnold tongues, named after Arnold of the KAM theorem, are regions in the phase space of circle maps with locally constant rational rotation (winding) numbers between the driver and the natural oscillator frequencies, p/q. They were first investigated for a family of dynamical systems defined by Kolmogorov, who proposed this family as a simplified model for driven mechanical rotors described by equation (1). The circle map of the equation exhibits certain regions in the parameters space when it is locked to the driving frequency (phase-locked, or synchronized). Here, q is interpreted as the polar angle such that its value lies between 0 and 1; the two parameters are K the coupling strength between the driver and the rotor, and W is driver frequency. A typical map with Arnold tongues is given in Figure 1.
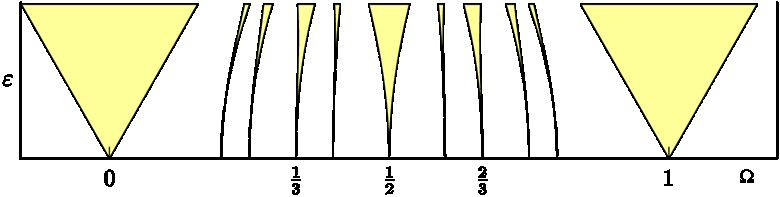
Figure 1 Some Arnold tongues in the standard circle map e = K/2p versus W
For small to intermediate values of K (0-1) and certain values of W, the map exhibits phase locking. In the phase-locked region, qn advances essentially in a rational multiple of n; although it may do so chaotically on the small scale.
The phase-locked regions, called Arnold tongues, are coloured yellow in Figure 1; while the quasi-periodic regions are white. Each yellow V region touches down to a rational value of W = p/q in the limit of K → 0. The values of (K, W) in one of these regions will all result in a motion with rotation number w = p/q. For example, all values of (K, W) in the middle V region correspond to w = ½. In other words, the sequence stays locked on to the signal despite significant noise or perturbation. This ability to lock on in the presence of noise is central to the utility of phase-locked loop electronic circuits.
The circle map in Figure 1 is invertible or symmetrical around the mid line.
The golden mean critical point
For values of K>1, the circle map is no longer invertible. In Figure 2a [9], the circle map is extended to K = 4. Arnold tongues of synchronization are in grey with winding numbers indicated inside the tongue. The white regions are quasi-periodic, and the stippled regions appearing beyond the line K = 1 represent chaos. (See the fully coloured version of this map at the beginning of this article.) This map also depicts fractal self-similarity on different scales. Fractal self-similarity and chaos are closely related. A chaotic system has a fractal dimension, i.e., a fractional dimension between the usual integer values, 1, 2, 3, or 4, and exhibit self-similarity over many scales.
It is important to note that chaos most definitely does not mean random. Mathematically, chaos is locally unpredictable and sensitive to initial conditions, but it is globally determined or bounded by ‘strange attractors’ (see later). There is no universally accepted or rigorous definition of chaos, and there are many interesting attempts at describing it (see [10]).
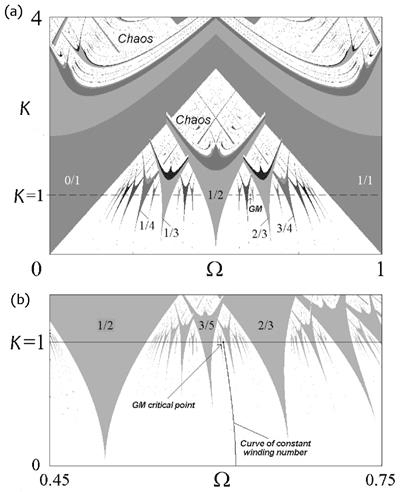
Figure 2 Extended circle map (see text for details)
The golden mean critical point (GM) is where the curve of constant irrational winding number f = (√5 -1)/2 terminates on the line K = 1 (see Fig 2b), and quasi-periodic behaviour undergoes transition to chaos. This point is marked by an infinite sequence of unstable orbits with periods given by the Fibonacci numbers (see [11] The Story of Phi Part 1, SiS 62) for the intimate connection between the Fibonacci sequence, where the ratio of successive numbers converges to the golden ratio).
The golden ratio is thus located at “the edge of chaos”, and has a role in keeping the system of oscillators active without interfering with one another as well as away from the state of chaos. Unfortunately, the term chaos has a much undeserved negative connotation, because of its association with the breakdown of order and total randomness, which it definitely does not involve.
So, is our solar system stable? There is good evidence that the planetary orbits around the sun exhibit golden ratios or ratios according to the Fibonacci sequence numbers, as many people have commented (see [12, 13] for example). The question is whether it will remain stable as such, at least for billions of years, or in transit to chaos much sooner than that. Some astrophysicists claim however, that the planetary orbits are chaotic and sensitive to initial conditions, hence unpredictable for longer than 100 million years into the future [14]; so there is still no immediate cause for alarm.
Edward Norton Lorenz, MIT mathematician and meteorologist is the generally acknowledged ‘father’ of chaos theory [15]. During the winter of 1961, Lorenz was running a climate model on the computer described by 12 differential equations, when he decided to repeat one of the runs with a small change. Instead of calculating to six decimal digits, he rounded that to three to save computing time, fully expecting to get the same results. But he didn’t. That was the beginning of his discovery of the “sensitive dependence on initial conditions” of chaotic systems, which he described as the “butterfly effect”. It makes long term weather prediction impossible. His ‘toy’ equations produced the ‘Lorenz attractor’ (Figure 3) (the prototype of ‘strange attractors’ associated with chaotic systems), which bears serendipitous resemblance to butterfly wings, and became the emblem of the chaos era that followed. Numerous ‘strange attractors’ have been created, mostly as computer artwork, beginning with the book by Clint Sprott [16]. But chaos theory has found applications in meteorology, physics, engineering, economics, biology and medicine.

Figure 3 The Lorenz attractor by Clint Sprott
The Lorenz attractor is a fractal, with self-similar structure on different scales. It has a fractal dimension of 2. 06215 - almost a 2-dimensional surface but not quite, as it cannot be flattened out - and lives in a space of at least 3 dimensions. It contains unstable periodic orbits that can be identified using various mathematical procedures [17], and can also be regarded as twisted or ‘knotted’ periodic orbits [18].
This brings us back to the importance of cycles in understanding natural processes. The Lorenz attractor (Figure 3) is a Poincare section of the dynamical system’s phase space, which gives a picture of how the trajectory of the system intersects with the section or the surface of the phase space. Poincare section is named after French polymath Henri Poincare (1854-1912), who excelled in all fields that existed during his lifetime, and was the one who laid the foundations of modern chaos theory with his research on the ‘three body problem’ (see earlier). Poincare also emphasized the importance of periodic orbits.
Chaos theory has been taken up enthusiastically in every field including quantum physics, in the form of ‘quantum chaos’, which tries to build a bridge between chaos in classical mechanics and the wavelike motion of electrons in atoms and molecules. Martin Gutzwiller, a leader in quantum chaos wrote [19]: “Phase space for a chaotic system can be organized, at least partially around periodic orbits, even though they are sometimes quite difficult to find.”

Figure 4 Turbulent flow generated by the tip vortex of the aeroplane wing shown up by red agricultural dye, Wikimedia
Chaos is typical found in turbulent flows of fluids, gases, and the atmosphere. Turbulence is traditionally regarded one of the most intractable problems in physics and mathematics. Mary Selvam, now retired as deputy director of Indian Institute of Tropical Meteorology in Pune, first proposed a theory of turbulent fluid flow based on fractal space-time fluctuations in 1990 (see [20]).
Selvam treats the fractal fluctuations on all space-time scales as a superimposition of a continuum of eddies or vortices. Large scale fluctuations result from the integration of smaller scale fluctuations within. The larger scale eddies grow by enclosing smaller scale eddies and the growth trajectory traces an overall logarithmic spiral flow path with the quasi-periodic Penrose tiling pattern for internal structure.
The ratio of radii or circulation speeds corresponding to the successive growth steps of the large eddy generating the geometry of the quasi-periodic Penrose tiling pattern is, of course, equal to the golden ratio f = 1.618..(see [11]). Interestingly, the turbulence created by the tip vortex of the aeroplane in Figure 4 does trace out a logarithmic spiral approaching the golden ratio.
Treating turbulence as a continuum of discrete eddies or cycles with Penrose tiling pattern of growth captures key features of organic spacetime. Cycles imply perpetual return, a regeneration conferring identity, stability and autonomy, the very signatures of life. My artist impression of fractal organic spacetime (Figure 5) could be readily interpreted in terms of larger eddies (activity cycles) enclosing smaller ones within; except for the quantum entanglement that takes it away from a perfect nested hierarchy.
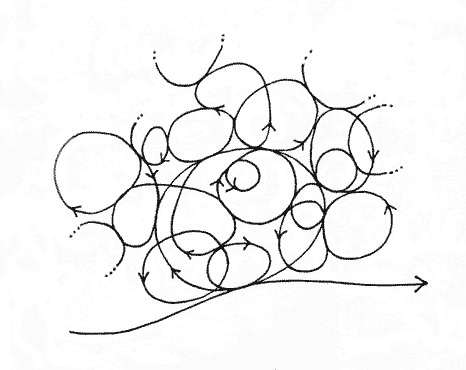
Figure 5 Artist impression of organic fractal and entangled spacetime (from [2])
English mathematician philosopher Alfred North Whitehead (1861-1947) was in no doubt that the entire Universe is a super-organism consisting of organisms on every scale from galaxies to elementary particles [21], and argued it is only possible to know and understand nature both as an organism and with the sensitivity of an organism. I have taken his words to heart, and benefited a great deal in my continual quest for the meaning of life.
This series will end with an amazing new vision of the universe [22] (Golden Geometry of E Infinity Fractal Spacetime, SiS 62) that brings us much closer to our intuitive feeling for organic spacetime.
Article first published 24/03/14
Comments are now closed for this article
There are 2 comments on this article.
www.gold-dna.de Comment left 25th March 2014 01:01:50
Thank you very much for spreading the word of PHI. I am looking forward to the last part in this series.
Anyone interested in PHI on an even deeper level can visit http://www.gold-dna.de/phi.html ... unfortunately in German, but worth the trouble ;-)
Guido Vobig
Scott Collimgwood Comment left 26th March 2014 18:06:05
Just in passing I think it's important to note that Buddhist cosmology is taken from the Vedic literature.