Science of the Organism
A non-mathematician describes her own initiation into the secrets of the magic number in the heart of mathematics, and how it is woven into the fabric of the physical and living world. Dr. Mae-Wan Ho
The golden ratio f (a Greek letter pronounced phi) is an irrational number, one that is impossible to express as a simple fraction; and it is the most irrational of all irrational numbers because it can’t even be approximated as a simple fraction. Yet it turns up everywhere in nature; from chemical bonds in molecules to branching trees, spiral galaxies, and fundamental quantum reality; it is embedded in our brain waves, in music, and of course, in the heart of mathematics (see [1-4] for example).
The numerical value of phi is 0.6180339…(continued on indefinitely), and is the solution to a problem that sounds so simple.
Suppose you have a line of any length, call it one. You need to divide it unequally, so that the ratio of the larger segment to the whole, 1, is exactly the same as that of the small segment to the larger (Figure 1).
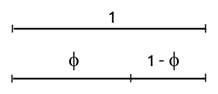
Figure 1 Golden ratio, the perfect cut
From Figure 1, we get the following:
f/1 = (1 – f)/f
f2 = 1 – f
f2 + f = 1
f2 + f - 1 = 0 (1)
Solving the equation (1) for f with the quadratic formula in basic algebra gives:
f = (√5-1)/2 = 0.6180339887…
The reciprocal of phi, represented by the same letter in capital f (Phi) is also often referred to as the golden ratio, and is equal to:
1/f = f = (√5+1)/2 = 1.6180339887…= 1 + f
Amazingly, precisely the same numbers occur in both ratios after the decimal. Not only that, squaring f gives 2 plus exactly the same numbers after the decimal
f2 = 2. 6180339887….. = 2 + f
I leave you to do more sums and work out other marvels of phi.
The golden ratio is the perfect cut. It gives self-similarity or recursiveness at successive scales, and is considered the hallmark of beauty and balance in art and architecture. Most of all, phi has a host of magical properties enough to possess generations of mystics and scientists alike, beginning with the ancient Egyptian pyramid builders, who might have followed earlier forebears of this esoteric knowledge, now lost in the mist of time. Most of what is known in modern times came via the ancient Greek philosopher mathematician Pythagoras (c570BC-c495BC) and mathematician Euclid (323-283BC).
And I am among the latest to be smitten.
Being a scientist, I am far less interested in numerology than in what phi tells us about the very fabric of nature and natural processes. But it will help to flesh out the mathematical picture before proceeding to nature and natural processes.
The Fibonacci sequence is a sequence of numbers beginning with 1, 1, or 0, 1, in which successive numbers are the sum of the two previous:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …
The sequence is named after Italian mathematician Leonardo Fibonacci (~1170-1250) who got it during his wide travels from Indian mathematics [5]. Fibonacci considered the growth of a biologically unrealistic rabbit population, assuming that a newly born pair of rabbits, one male, and one female, are able to mate at the age of one month, so that at the end of the second month the female produces a fresh pair of rabbits (one male and one female), and the same for every month thereafter, as the rabbits never die. The question was: how many rabbits would there be at the end of the year?
Starting from a single pair the following sequence of events takes place to build up the population.
At the end of the first month, they mate, but there is still only one pair.
At the end of the second month, the female gives birth to one pair, so there are 2 pairs.
At the end of the third month, the original female gives birth to a second pair, and this makes 3 pairs.
At the end of the fourth moth, the original female produces a third pair, but the first pair of her offspring will also have produced their first offspring pair, making a total of 5 (Figure 2). At the end of the nth month, the number of pairs of rabbits equals to the number of new pairs (the number of pairs in month n-2) plus the number of pairs alive last month (n-1). This is the nth Fibonacci number:
Fn = Fn-1 + Fn-2. (2)
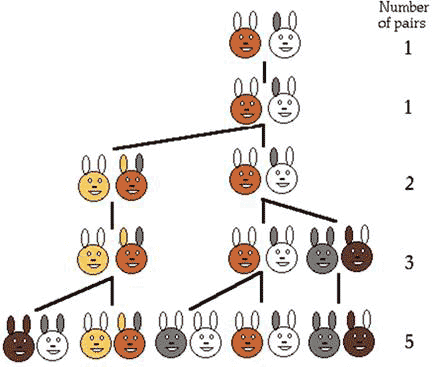
Figure 2 Growth in a population of imaginary rabbits follows Fibonacci sequence [4]
It was Johannes Kepler (1550-1517) who showed that the golden ratio is the limit of the ratio of consecutive Fibonacci numbers. In other word, the ratio of successive numbers get closer and closer to the value of the golden ratio as the sequence is continued ad infinitum. Now we know why phi is the most irrational of all irrational numbers.
The relationship of the Fibonacci sequence and the golden mean to growth with long-range correlation is seen in the spirals of Figure 3 [5]. As the spiral gets bigger and bigger it becomes more and more similar to the golden spiral, one version of which is constructed from an initial golden rectangle divided into squares (Figure 4).
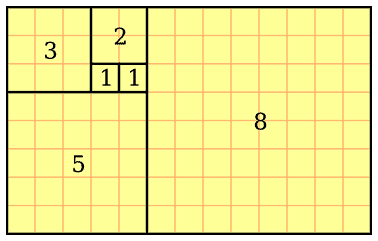
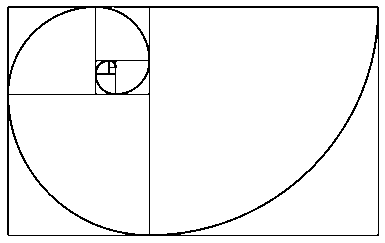
Figure 3 A spiral tiling with squares whose side lengths are successive Fibonacci numbers; the right diagram uses the squares of sizes 1, 1, 2, 3, 4, 8, 13, 21, and 34, and draws the quarter circle that fits into the squares; it approximates a golden spiral more and more as the Fibonacci numbers get bigger
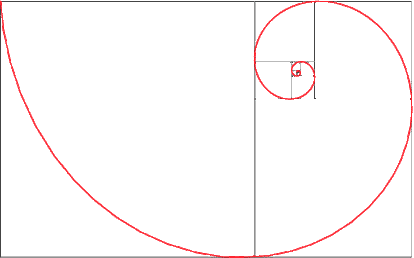

Figure 4 A golden spiral constructed by dividing an original golden rectangle into squares (left) and the Nautilus shell sectioned (right)
Both the Fibonacci spiral and the golden spiral approximate a logarithmic spiral, but is not actually a logarithmic spiral; and in mathematics, even the golden spiral is not considered the real golden spiral. A real golden spiral is a logarithmic spiral whose growth factor is Phi. It gets bigger and further from its origin by a factor of f for every quarter turn or 90° [6]. The equation in polar (circular) coordinates for a logarithmic spiral is
r = aebq (3)
where r is the radius, e is the base of the natural logarithm, a an arbitrary positive constant, b the growth factor and q the angle traversed. For the golden spiral, the golden ratio comes in when q is a right angle: ebqright = f. So, the real golden spiral is not a strictly a logarithmic spiral after all, as the growth between right angles are interpolated. The Nautilus shell (Fig. 4 right) consisting of successive chambers and grows according to the logarithmic spiral, but by a factor of the golden ratio f for each complete turn of the spiral, rather than a quarter turn.
The problem of tiling is to completely cover a surface area, as you would with tiles, and the golden ratio is a key to the problem, especially if you want interesting patterns that are not just based on squares. Tiling is easily done with squares (4 sides), or triangles and hexagons (3 and 6 sides). But it was long believed impossible to fill an area with 5 sided tiles or pentagons.
In the early 1970s, British mathematical physicist Sir Roger Penrose discovered that a surface can be completely covered in an asymmetric, non-repeated, and aesthetically highly pleasing way, using just two different shaped tiles derived from the pentagon [7]. Figure 5 shows two variations. You can flip the tiles and get many other patterns.
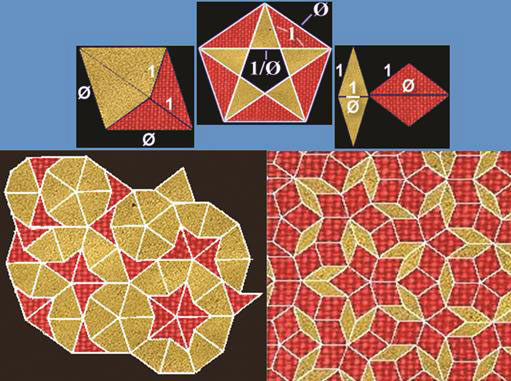
Figure 5 Penrose tiling based on the pentagon and the golden ratio (rearranged from [4])
The pentagon not only embodies the golden ratio, the resulting tiling also has a golden ratio of area covered by one kind of tile to the other. Five-fold symmetry is especially common in living organisms, and also exists in the enchanting world of quasicrystals, although it is absent from crystals (see [8] Golden Mean Wins Chemistry Nobel Prize, SiS 52).
In the rest of this series, we shall be exploring how the golden ratio is literally woven into the fabric of life and the universe.
Article first published 03/03/14
Comments are now closed for this article
There are 6 comments on this article.
James Cooley Comment left 4th March 2014 04:04:16
George Gamow wrote about a hierarchy on infinite sequences based on mapping one onto another. Might be relevant.
John Haughton Comment left 4th March 2014 23:11:28
Fibonacci seems to be the template that life uses to grow wherever you look. Almost all higher life starts with the union of male and female. Yin and Yang.
0 is clearly a female symbol, the seed, the empty womb of creation and 1 is a phallic male symbol.
In the Fibonacci series you start by adding (mating) 0 and 1 to produce another 1. This new "one" then grows and progresses in accordance with the rest of the Fibonacci series
0 + 1 -> 1, 2, 3, 5, 8, 13, 21...
http://www.youtube.com/watch?v=0tAZe6pP-FM
drew hempel Comment left 7th March 2014 17:05:39
Kepler was against the "closed form" solution of the Golden Ratio, believing instead that numbers were male and female, infinitely and that sacred geometry was not represented by number, instead being transcendent. This was also the view of the "divide and average" math of the Vedic sacred geometry and similar views elsewhere.
The closed solution has to reverse infinity - so that A to B as B is to A plus B has to be changed to "A minus B" - otherwise the original Fibonacci series can not be solved as a closed solution. The problem with this is that it covers up the inherent complementary opposites of number - known by the Taoist and by the real Pythagoreans.
The solution for this is from music theory, understanding complementary opposites so that the conversion of continued proportions to irrational numbers was from 1 is to 5/4 as 5/4 is to 8/5 is to 2 with 8/5 approximating the golden ratio and 5/4 approximating the cube root of two.
So three dimension geometry actually arises from two dimensional holographic quantum information as number with the original series - as infinite - the golden ratio as a continued fraction - 1 plus 1 divided by 1 infinitely. So that as the Taoists and Pythagoreans and Egyptians knew - the number 2/3rd is sacred as yang. 2/3 being the second term for the divide and average solution to the golden ratio.
My blogbook goes into more details: "the Alchemy of Rainbow Heart Music: How Paranormal Sonofusion Subverts the Matrix Conspiracy" - it's a free read pdf download online. thanks.
drew hempel Comment left 7th March 2014 17:05:14
Actually my new blog is more clear on this subject - http://innersoundqigong.blogspot.com but essentially the Golden Ratio assumes number as a symmetric materialism - magnitude as dimension. Quantum physics as the foundation of reality shows that number is actually asymmetric - complementary opposites based on the Fourier Uncertainty Principle - with zero time as infinite energy. This can be explained through music theory which again is the missing factor at the origin of the "Greek Miracle" as math professor Luigi Borzacchini discovered. So the tritone music interval was the origin of the square root of two as the first irrational number from 9/8, the major 2nd, cubed. Again this assumes time is a symmetric geometric measurement thereby covering up and lying about the true assymetric complementary opposites of number - yin and yang dynamics. So that the Perfect Fifth is yang as 2:3 subharmonic C to F while as 3:2 overtone it is C to G. So it is non-commutative just like with quantum uncertainty. It is infinite and formless - and can not be contained by geometry. So the Golden Ratio is from quantum chaos - after the Poisson Bracket is applied.
Todd Millions Comment left 12th March 2014 15:03:00
Behold-HMS Coxeter, explaining the oh so elegant George Odam construction-How'd everone miss this?
Sanjuanita Comment left 22nd September 2016 23:11:35
Lovely article - one of the best things I've recently read, and by far the most useful. You touched on a topical issue.