Science of the Organism
The spiral arrangements of plant elements around the stem are based on the golden ratio; asking why leads us on to a deeper realm of beauty Dr. Mae-Wan Ho
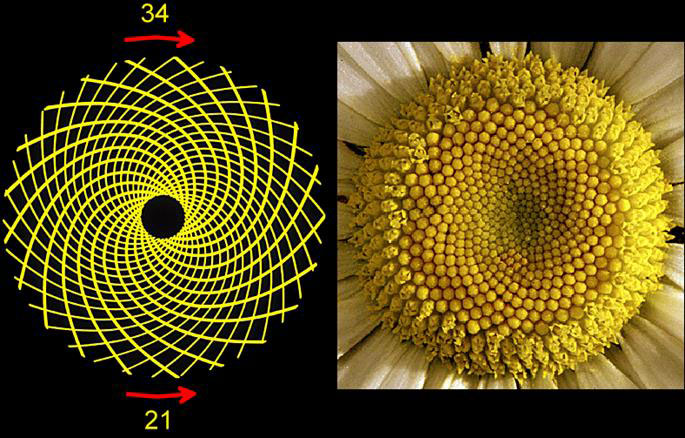
Florets in a daisy with 21, 34 parastichy (see text)
In the study of plants, one of the most abiding puzzles is phyllotaxis, the arrangement of leaves, flowers, petals, or florets around the stem. This problem fascinated British mathematician, computer-pioneer, and code-breaker Alan Turing (1912-1954), and from an early age. A sketch made by his mother showed him distracted from his cricket game “watching the daisies grow.” Tragically, Turing committed suicide before he could solve the problem [1, 2], after having been convicted of homosexuality and forced to undergo ‘hormone therapy’. It was not until 2009 that British Prime Minister Gordon Brown made an official public apology on behalf of the British government and 24 December 2013 that Turing received a posthumous pardon [3].
Spiral phyllotaxis is common among plants. An example is the succulent plant Aeonium (Figure 1 [4]). The leaf-like elements come out one by one from the growing tip of the main stem, each at a constant divergence angle d from the previous, which is often close to the golden angle 137.5°, derived from the golden ratio F = 1.618; the actual angle is 360/1.618 = 222.5°, but it is usual to recognize the smaller reflex angle of 360-222.5 = 137.5°.

Figure 1 The Aeonium plant showing spiral phyllotaxis (left) with successive leaf-like elements coming off the main stem at an angle of approximately 137.5°, the golden angle [4]
When two or more elements come off a single node (or tier), referred to as multijugate phyllotaxis, each whorl is at a constant divergence angle from the previous.
To classify the multijugate patterns, we count the number of spirals joining each element to its nearest neighbours . This gives a pair of numbers, one for the spirals going counterclockwise, and the other, the spirals going clockwise; the pair of numbers is the parastichy. Thus, the Aeonium plant in Figure 2 has a 2,3 parastichy, there being 2 spirals in the counterclockwise direction and 3 in the clockwise direction. The two numbers are successive members of the Fibonacci sequence (see [5] The Story of Phi, SiS 61).

Figure 2 The Aeonium plant has a 2, 3 parastichy [4]
When the elements are tightly packed, there are many more spirals. The cauliflower (Figure 3) has 8 counterclockwise and 13 clockwise spirals, giving an 8, 13 parastichy; the daisy at the beginning of this article shows florets in the centre in 21 counterclockwise and 34 clockwise spirals, giving a 21, 34 parastichy. These pairs are also successive numbers in the Fibonacci sequence.

Figure 3 Cauliflower with 8, 13 parastichy
Scottish biologist, mathematician, and classic scholar D’Arcy Thompson (1860-1948) already established early in the last century that the angle between successive elements in the tightly wound spirals approximate the golden angle 137.5° based on Phi [6]. But no satisfactory explanation was forthcoming for a long time. Many trivial suggestions include adaptation and natural selection, or design by god; as the arrangement optimises reception of light for photosynthesis.
From the snug way in which the florets fit together in the heart of the daisy, it would appear that the golden ratio and associated Fibonacci spirals do result in the optimum packing. This is easily demonstrated using a computer generative algorithm developed jointly by the research teams of Przemyslaw Prusinkiewicz at University of Regina, Saskatchewan in Canada, and Astrid Lindenmayer at University of Utrecht in The Netherlands [7]. Remarkably, the optimum packing arrangement closest to the actual daisy is generated only when the divergence angle of 137.5 is used; slight deviations on either side result in very different patterns with large gaps between spirals (see Figure 4). This space-filling capacity of the golden ratio is very significant, as in the Penrose tiling (see [1]), and we shall come back to it again in later articles of this series. It also gives a feeling of balance and beauty.

Figure 4 Phyllotaxis patterns generated on a disc with divergence angle 137.3° (a), 137.5° (b) and 137.6° (c)
However, the importance of the golden angle still does not explain how it arises, without invoking divine design or its equivalent in neo-Darwinian ‘selective advantage’; for even if the particular arrangement of leaves and florets does benefit the plant, one needs to explain how the form was generated in the first place. We need to understand the mathematics, physics, chemistry and biology.
In 1992, French mathematicians Stéphane Douady and Yves Couder at CNRS (French National Centre for Scientific Research) Paris made a breakthrough. They showed that the patterns arise spontaneously as the result of a simple growth process in which primordia appear periodically near the tip of the growing shoot and are pushed away (advected) from the centre as the tip elongates [8] (or perhaps equivalently, increase in diameter). Identical elements are generated with a periodicity T at a given radius R0 from the centre and advected at velocity V0, and there is repulsion between them, so new elements will appear as far as possible from the previous one. The results could be interpreted with a simple equation consisting of only one (dimensionless) parameter G = V0T/R0.
To model the process physically, Douday and Couder set up a petri dish with a central cone fill with some viscous silicone oil, and release drops of ferroliquid onto the cone, which are advected towards the periphery by a magnetic field (Figure 5).
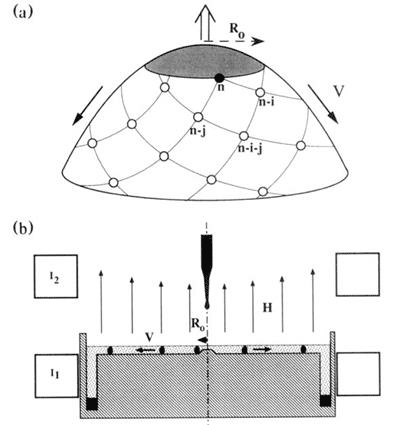
Figure 5 Diagram of the growth zone with successive primordial (a), and experimental model of the process (b) (from [8])
When advection is strong, each drop is repelled by the one before and goes to the direct opposite (180°). But as G decreases (advection slows, or equivalently, the period between primordia shortens, each will be influenced by the two previous, and will go in the space between them at an angle of 150°. As G decreases further, each drop will be influenced by three or more previous, and the angle becomes 139°, quite close to the golden angle, when the spirals take on the Fibonacci values 3 and 5. The process approaches the golden ratio in the limit. It ends up filling the entire available space, creating a structure of minimum global interaction energy, a natural balance between opposing forces and tensions, which is where beauty lies.
The research also shows that the process gives reliable results regardless of the detailed biological or physical mechanisms; these characteristics of reliability, robustness and genericity are intimately associated with the balance and dynamic equilibrium embodied in the golden ratio, the kind of beauty and elegance that seduce scientists and mathematicians.
The results were also successfully simulated by computer and can be used as the most natural system for classifying plants and animals sought by Swedish botanist and physician Carl Linnaeus (1707-1778) and generations of taxonomists after him [9].
Article first published 10/03/14
Comments are now closed for this article