Water's Quantum Jazz
Other reports in this series
Cooperative hydrogen-bonding between molecules gives rise to energetically favourable three-dimensional network of supramolecular clusters in liquid water under ambient conditions, resulting in long-range dipole correlation and quantum coherence Dr. Mae-Wan Ho
As a self-confessed hydrophiliac, I love nothing more than to immerse myself in water, literally and figuratively. I have been obsessed with water’s unfolding biopic as though my own life depends on it, and most certainly so (see [1] Two-States Water Explains All? SiS 32, and other articles in the long running New Age of Water series). Water is the simplest, commonest chemical compound on earth. Yet, it has the most complex properties and baffling ‘anomalies’ compared to its neighbours in the periodic table of chemical compounds, without which life as we know it would be impossible. Water has remained a mystery to generations of the best scientists who have pitched their wits (and sophisticated instruments) at water, only to have it slip gracefully through their fingers.
Water is perfectly transparent and has no colour, except when its fine droplets refract sunlight into the dazzling spectrum of the rainbow. Water has no form other than that of the containing vessel, no sound, no movement, and little resistance; except when coaxed by the gentle breeze into smiling ripples, or tickled into undulating waves lapping like laughter. Or else when whipped up by hurricanes into howling surges that hurl ships into the air, or heaved by submarine earthquakes into rumbling tsunamis that deluge shore and land.
The dramatically different, infinitely varied moods of water are the stuff of life itself, if not also great art. Indeed, a good scientific theory needs to capture the art, to explain the long range cohesion coalescing massive volumes into gigantic whirlpools, and at the same time bespeaks the endless diversity in molecular structures that makes every snowflake a unique event in the history of the universe (see [2] Crystal Clear – Messages from Water, SiS 15).
This latest episode brings together evidence, old and new, that confirms what many of us had suspected: water is coherent, if not quantum coherent, and it is that which accounts for all its life-giving properties. We begin with some basics on which almost everyone agrees.
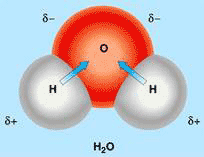
Figure 1 The water molecule with separated positive and negative charges
The water molecule is a permanent dipole in which positive and negative charges are separated, with the two hydrogen atoms at the positive pole and the oxygen atom at the negative pole (see Fig.1). Like other dipoles, water molecules can stack together in dipole interactions with alternating positive and negative poles next to each other. It can also engage in electrostatic interactions with charged ions and other dipoles dissolved in it.
In addition, the water molecule likes to hydrogen-bond with one another (Fig. 2), and with molecules and ions dissolved in it. A hydrogen bond consists of hydrogen shared between two electronegative atoms such as oxygen or nitrogen. The compound or group that donates the hydrogen is the hydrogen donor, while and compound or group that accepts the hydrogen is the hydrogen acceptor. Water is both hydrogen donor and acceptor; it can donate two hydrogens and its oxygen can accept two other hydrogens. The water molecule is generally represented as a tetrahedron with four ‘arms’ – two hydrogen donors and two hydrogen acceptors - pointing at the vertices. This tetrahedral structure is typical of ordinary ice, where all the water molecules are cross-linked in a crystalline, hexagonal array (see below).
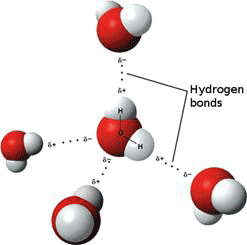
Figure 2 Hydrogen-bonded water molecules
Decades of research has resulted in a near-consensus that water at ambient temperatures and pressures exists as a dynamic network of supramolecular clusters where a proportion of the molecules are linked together by ‘flickering’ hydrogen bonds, similar to those in ordinary ice. It is also widely acknowledged that the hydrogen-bonded network of liquid water accounts for most, if not all its anomalous properties. Beyond that, there is no agreement over the exact proportion of molecules linked by tetrahedral ice-like bonds, the precise structure and size of the clusters, how freely the molecules can move around, and especially whether interactions are strictly local with nearest neighbour, or much more global in extent.
Within the past decade, substantial evidence has emerged indicating that cooperative interactions between molecules results in remarkably long-range coherence in liquid water under ambient conditions.
First of all, water has an unusually high dielectric constant of ~78 at room temperature, making it the most important polar solvent in chemistry and biology, it also means it is easily polarised by an electric field. The dielectric constant, or relative static permittivity, is a measure of the extent to which it concentrates electrostatic lines of flux relative to a vacuum. Researchers led by Manu Sharma at Princeton University, New Jersey, USA, have shown by molecular dynamics simulations from first principles that the high dielectric constant of water is due to two effects of the hydrogen bonds contributing in almost equal measure [3]. The hydrogen bonding serves to align the dipoles and at the same time, pull away positive and negative charges within a molecule, enhancing the average molecular moment.
Cooperativity in chemistry is the tendency of individual chemical interactions to influence each other, so that local actions can have global effects, and vice versa; the whole being greater than and not predictable from the sum of the parts. That’s how organism work, and why water is so vital for life (see [4] Quantum Jazz Biology, SiS 47).
Quantum chemist Roger A. Klein at Bonn University in Germany has demonstrated from electronic and quantum chemical computations that cooperativity is involved in the formation of hydrogen-bonded supramolecular clusters [5].
Different forms of ice are all variations on the theme of tetrahedral molecules arranged in the form of hexagons, or six-member rings, as determined by X-ray and neutron diffraction. It is therefore reasonable to think of liquid water as flickering clusters of interlocking hexagonal rings, with some long range order extending on average to at least the second or third nearest neighbour; which is compatible with data from X-ray or neutron scattering experiments (see [1]).
In gas clathrates – where gases such as methane are caged in ice at the bottom of the Arctic Ocean – the water molecules tend to form pentagonal arrays of cages fused along the edges.
Cooperativity is involved in the formation of the six- and five-member rings, as evident in the greater stabilizing energy and higher electron density at ‘bond critical point’ (bond strength) for each hydrogen bond in the cluster compared to a single hydrogen bond between two water molecules (dimmers). The higher electron density and bond strength is a consequence of the shortening of the hydrogen bonds within the cluster compared with that in a dimer (Fig. 3).
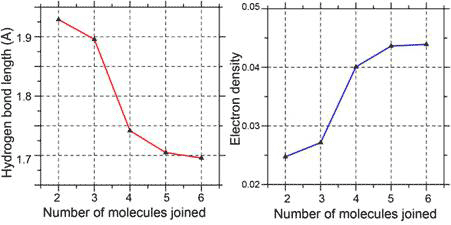
Figure 3 Cooperativity shortens (left) and strengthens the hydrogen bonds (right)
Increasing cooperativity is more associated with a greater proportion of tetrahedral ice-like bonds in water clusters than with cluster size alone, once an optimal ring size of five or six water molecules has been reached. Thus, it is no accident that the hexagonal motif is common in liquid water and ice, and the edge-fused pentagonal motif in gas clathrates. Both are optimised for cooperative interactions, which in turn make it likely for large clusters to form. There is evidence that large clusters actually exist in liquid water under ordinary conditions, making coherent energy transfer possible.
At a temperature of 300 K (≡ 27 ˚C), ~90 percent of water molecules are hydrogen-bonded, a picture supported by molecular dynamics simulations and a large body of experimental evidence [6, 7]. The structure of the hydrogen bond network fluctuates on time scales ranging between 10 fs (femtosecond, 10-15 s) and ~10 ps (picosecond, 10-12 s), and includes changes of molecular orientations and distances, hydrogen bonds breaking and reforming, and slower rotational motions.
The O-H bond stretch vibration exhibits a 270 cm-1 wide band (in wave number, an alternative way of expressing frequency) centred at ~3 400 cm-1 in the infrared region. As temperature decreases, the maximum of the band shifts to lower frequencies and the envelop changes shape, indicating an overall enhancement of hydrogen bonding. The O-H bond stretching vibration is a sensitive indicator of structural and dynamical fluctuations in the extended hydrogen-bonded network.
Two-dimensional infrared photon echo (2DIR-PE) spectroscopy has been added recently to the armoury of techniques for probing water. The technique depends on exciting (pumping) the O-H bond stretching vibration with infrared light, and looking for the response (echoes) in the infrared spectrum.
Using 2DIR-PE spectroscopy, researchers at the University of Toronto, Canada, and Max-Born Institute for Nonlinear Optics in Berlin, Germany, discovered ultrafast resonant transfer of excitation energy between water molecules that takes place via dipole coupling in the hydrogen-bonded network [6]. The energy transfer time of ~80 fs is unaffected by temperature from 340 to 274 K [7]. This transfer time in pure water is substantially faster than the 700 fs previously measured in a D2O:H2O mixture, where resonant energy transfer is obstructed, and is also much shorter than the average hydrogen bond lifetime of ~1ps.
The experiment carried out at different temperatures [7] showed that frequency correlations (between excitation and echo) due to local structures are lost in about 50 fs at high temperatures (hinting at a much more flexible hydrogen-bonded network). But at lower temperatures these correlations are longer-lived. At 274 K (just above freezing), a dramatic change takes place, and the frequency correlations persist beyond ~200 fs, indicating that the hydrogen-bonded supramolecular structures are stabilized.
Liquid water at ambient temperatures is traditionally regarded as a homogeneous phase, with the same average structure everywhere. However, some scientists, beginning with Wilhelm Conrad Rőntgen who won the 1901 Nobel Prize for the discovery of x-rays, believe that the anomalies of water are best explained if liquid water is an equilibrium mixture of two states that differ in density [1].
Recently, researchers at Stanford University in California, USA, provided fresh evidence that liquid water is indeed inhomogeneous over a length scale of about 1 nm [8]. Combining small angle x-ray scattering, which gives information on the size of supramoleular structures, with x-ray emission and x-ray raman scattering, which yield information on hydrogen bonding, the researchers were able to show that water at ordinary temperatures exists in two distinct states (with no intermediates): low density water (LDW) in which the molecules are hydrogen-bonded in ice-like tetrahedral bonds; and high density water (HDW) in which the molecules are linked by more distorted hydrogen-bonds. Hence, density fluctuations occur over the length scale of ~1.2 nm.
The length scale of ~1.2 nm encompasses about 70 molecules of water. It is tempting to equate that with the inner core of Martin Chaplin’s icosahedron containing 280 molecules of water, which he has proposed as the predominant supraomolecular structure of water under ambient conditions [1]. The icoshedron is composed of 20 identical units of 14 hydrogen-bonded molecules, five of which are in the inner core.
At 24 ˚C, the proportion of light water with ice-like tetrahedral bonds is about 28.6 percent [7], and only disappears completely at boiling point.
More and more researchers are coming around to the view that quantum effects need to be taken into account in molecular dynamic simulations of water in order to reproduce and interpret a range of experimental results [9]. Kim Hyeon-Deuk and Koji Ando at Kyoto University, Japan, believe that quantum effects play a key role in the dynamics of the hydrogen-bonded network, and are therefore essential for understanding the anomalous properties of water [10].
Nuclear quantum effects – effects due to the nuclei of atoms - have a significant impact on the behaviour of water. This is evident in the large changes observed in numerous properties of water when hydrogen (H) is substituted by its heavier isotopes deuterium (D) and tritium (T). For example, the melting of D2O is 3.82 K higher than that of ordinary water, and the effect is even more pronounced in T2O.
Evidence for nuclear quantum effects in water is steadily growing. Recently, researchers at several institutes in Madrid, Spain, demonstrated that nuclear quantum effects have to be included in molecular dynamic simulations in order to reproduce experimental heat capacity measurements over a wide range of temperatures encompassing ice and liquid water. They regard the heat capacity of water “a signature of nuclear quantum effects” [11].
Francesco Paesani and colleagues at the University of California La Jolla, USA, investigated the molecular reorientation associated with the dynamics of the hydrogen-bonded network in liquid water using quantum molecular dynamic simulations. They found the calculations in excellent agreement with the corresponding experimental results obtained at different temperatures with polarization resolved, femtosecond infrared, spectroscopic measurements [12]. Comparison with the results obtained using classical molecular dynamics simulations clearly indicated that the explicit inclusion of nuclear quantum effects is critical for reproducing the experimental results.
Water not only possesses quantum properties; it may actually be or become quantum coherent. Evidence for quantum coherence in water has come from unexpected observations in nuclear magnetic resonance experiments (see Box) over the past twenty years. These are intermolecular multiple quantum coherence signals generated by the collective effects of the dipole coupling of the spin of each molecule with that of every other in the sample, up to 1 millimetre apart [13, 14]. This implies that all the spins of the molecules in the sample are correlated, and driven by the same (electromagnetic) field to oscillate in phase [15-17].
Nuclear magnetic resonance (NMR) spectroscopy is a technique that exploits the magnetic properties of certain atomic nuclei possessing spin, such as protons 1H and 13C. All stable isotopes that contain an odd number of protons and/or of neutrons have an intrinsic magnetic moment and angular momentum or spin; while all nuclei with even numbers of both have spin 0. When placed in a magnetic field NMR active nuclei absorb at a characteristic frequency, depending on the strength of the magnetic field [18]. For example, in a 21 Tesla magnetic field, protons resonate at 900 MHz. In the earth’s magnetic field, these nuclei resonate at audio frequencies (20 to 20 000 Hz). The effect is exploited in Earth’s field NMR spectrometers and other instruments that are portable and inexpensive, and often used for teaching or field work.
Depending on the local chemical environment, different protons in a molecule resonate at slightly different frequencies. As both the frequency shift and the fundamental resonant frequency are directly proportional to the strength of the magnetic field, the shift is converted into field independent dimensionless value known as the chemical shift, measured from some reference resonance frequency. For the nuclei 1H and 13C and 29Si, TMS (tetramethylsilane) is commonly used. This difference between the frequency of the signal and the frequency of the reference is divided by the frequency of the reference signal to give the chemical shift. As the shift is generally very small, it is expressed in parts per million (ppm).
In NMR imaging, a magnetic field gradient is used, and the resonance signal depends on where in the gradient field the sample is located.
The magnetic nuclear spins of the sample is first aligned in a constant magnetic field. Then the alignment is perturbed by a radio frequency (RF) pulse. The two fields are chosen to be perpendicular to each other as this maximizes the NMR strength. The process called population relaxation refers to nuclei that return to the thermodynamic state in the magnetic field. This is the t1 spin lattice or longitudinal magnetic relaxation, t1 being the mean time for an individual nucleus to return to its thermal equilibrium state of the spins. Once the nuclear spin population is relaxed, it can be probed again with another RF pulse. The perturbed nuclei begin to spin at the resonant frequency, and precess (gyrate) until they fall out of alignment with one another and stop producing a signal. This is called t2 or the transverse relaxation time. t1 is always longer than t2 because of smaller dipole-dipole interaction effects. In practice, the value of t*2 is the actually observed decay time of the NMR signal.
Most applications of NMR involve full NMR spectra. Short square pulses of a given carrier frequency contains a range of frequencies centred about the carrier frequency, with the range of excitation (bandwidth) being inversely proportional to the pulse duration. Applying such a pulse to a set of nuclear spins simultaneously excites all the single-quantum NMR transitions, causing precession about the external magnetic field vector at the NMR frequency of the spins. This oscillating magnetization vector induces a current in a nearby pickup coil, creating an electrical signal oscillating at the NMR frequency. This signal is known as the free induction decay and contains the vector sum of the NMR responses from all the spins. Fourier transformation of the signal gives the frequency spectrum.
Using pulses of different shapes, frequencies and durations in specifically designed patterns or pulse sequences allows the scientist to extract many different types of information about the molecules. Multidimensional NMR spectroscopy involves at least two pulses, and as the experiment is repeated, the pulse sequence is varied.
Warren and collaborators discovered in the 1990s that it was possible to observe intermolecular multiple-quantum effects in simple liquids using pulse sequences that involve as few as two RF pulses. High orders (degrees) of quantum coherence in water have been detected in simple experiments. In one of these, a 90˚ RF pulse is followed immediately by a gradient pulse (see Box) to code the induced coherences; after a delay D of 150 ms, a second 90˚ RF pulse is applied to make the coherence observable, and the coherence of order n is selected with a second gradient pulse of the same amplitude lasting n times as long as the first. The echo signals are shown in Figure 4 [19].
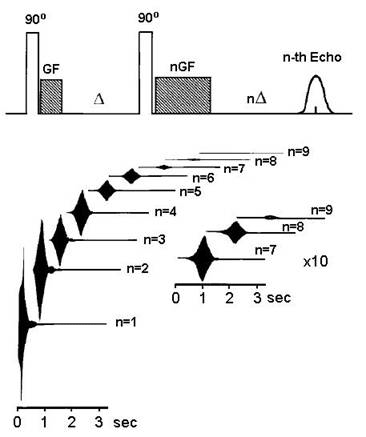
Figure 4 High order intermolecular quantum coherence in water detected by NMR
These remarkable findings have resulted in significant contrast enhancement in magnetic resonance imaging and functional imaging [20, 21], and many other applications. But their fundamental significance – that water is quantum coherent to a high degree – has remained unappreciated by the general scientific community.
The possibility that naturally occurring water may be quantum coherent should be considered in the light of the ambient magnetic field of the earth to which the water is constantly exposed. At the strength of the earth’s field, nuclei including protons would resonate at audio frequencies (see Box). Could it be that these natural nuclear magnetic resonances have vital biological consequences, including the possibility of homeopathy? (See [22] Electromagnetic Signals from HIV, Prospects for a Science of Homeopathy, SiS 48.)
For me, the most convincing evidence of water’s coherence has come from an extraordinary and brilliant French artist Michel Kappeli, who wrested the hidden symphonic structures made by the water flowing in his local river ([23] Water, Uncharted Spaces – the Body of the Transitory, SiS 48). His method was simply to allow water to speak directly, unmediated and unobstructed by opaque instrumentation. He said, “To capture a purest possible image of the flux, it was most important to reduce technical aids as far as possible,” and resort to aesthetic imagination, he might have added.
Article first published 27/09/10
Comments are now closed for this article
There are 3 comments on this article.
patrons99 Comment left 28th September 2010 04:04:35
I'm reminded of the scene from the film Waterworld, when Kevin Costner is dumped into some toxic bilge up to his neck. Well, this is what pharma's vaccine schedules and mainstream medicine are doing to us. You can also analogize it to pumping millions of gallons of crude oil, heavy mud, and detergents into the Gulf of Mexico and hoping it will all work out for the best for the environment.
Linus Pauling's work on protein structure was prescient. He foresaw epigenetic control of gene expression and the importance of the Terrain. Something as simple as a pH change, a hydrogen bond, an electrostatic interaction, a hydrophobic interaction, could horribly disrupt our internal God-designed equipoise. The current epidemic of vaccine-induced diseases was completely predictable.
patrons99 Comment left 28th September 2010 15:03:56
Yet another VERY thought provoking article in the series, Dr Ho! Thank you!
When doing proton NMR spectroscopy, you typically dissolve your bioorganic sample in deuterium enriched water - heavy water - so that the proton chemical shifts of the biomolecule are not drowned-out by the much stronger proton signal of the water in which the sample is dissolved. Even with highly deuterium-enriched water, there is usually still a discernible water signal. Your article and your hypothesis that in vivo water is quantum coherent to a high degree is VERY provocative. The water signal itself has a variable half-width of chemical shifts. The water signal undoubtedly has a strong temperature dependence, too. Now I'm not a physicist, but I recall that if you pulse a magnetic field you create a magnetic field gradient which induces a microcurrent of electric charge. Might these microcurrents somehow disrupt the metabolic pump activity that is necessary for sustaining life?
http://altered-states.net/barry/bobbeck/einstienmedical.htm
It's a bit off-topic, but where do you suppose the antimicrobial properties of colloidal silver derive?
http://liquidcolloidalsilver.net/colloidal-silver-uses-natural-antibiotics
Savita Pundlik Comment left 22nd June 2011 21:09:56
I found this article extremely useful since many aspects on water structure are briefly and very well described.